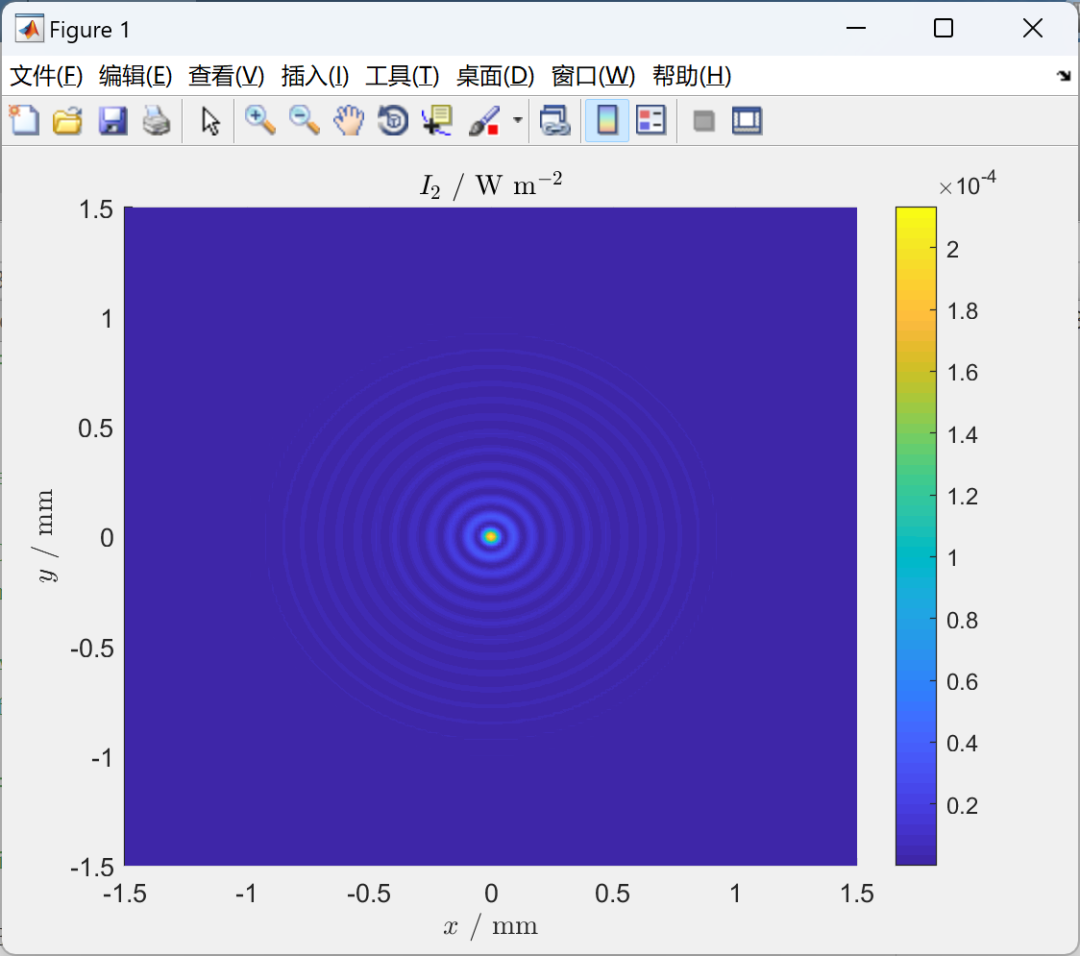
激光干涉测量——这一看似深奥无比且具高大上科技感魅力的技术,实则已成为当代精密测量界的领军者。这项基于激光特性并借由干涉现象精确描绘长度与位移的技术,其测量精度之高足以令世人瞠目结舌。然而,在追求亚纳米级精度的道路上,这项技术的运用并非一路坦途。光的衍射效应,这个光学世界中的常客,开始在测量过程中制造麻烦,引发系统误差,从而对测量结果产生负面影响。
激光干涉测量的基础知识
试想一下,一束光穿梭于空气之中,当其撞到某个物体时,光线会发生反射,再次返回并与原态并合,进而产生干涉效应,犹如一场光的曼舞,波峰与波谷交汇,形成明暗交替的条纹。这些条纹正是我们度量长度的关键所在。然而,在这一过程中,光的衍射效应如同舞台上的意外,扰乱了原本优美的舞步,从而对测量结果造成了误差。
衍射效应的挑战
衍射,作为光学领域的常客,时常在我们不经意间引发困扰。光线穿越小孔或边缘后,将产生扩散并构建新波前,这在日常环境无处不在,例如透过树叶的阳光以及夜间远处的车灯。然而,在精确度要求甚高的测量过程中,此类扩散效应往往会导致测量误差,特别是在追求亚纳米级别精度的情况下,其影响更不可忽视。
标量近似的局限性
以往,科研工作者常运用标量近似法,默认光波仅具有单一振动方向,进而忽视其矢量性质。然而,现今追求精密测量的要求让这一线性化策略显露弊端,光矢量特性,尤其其偏振态,对测量结果产生显著影响。
偏轴近似的不足
偏轴近似法乃是常用于简化计算的途径之一,其假定光线在传递时始终维持平直的波前形态。该方法适用于绝大部分普通光学系统,然而当面对复杂干涉仪中的多重反射与折射现象,以及非平面或球面波动的波前,偏轴近似法或许无法精确描绘出光线的传播轨迹,从而引发测量误差。
惠更斯积分的引入
针对此类难题,科研团队正在尝试创新手段。表面上看起来难以捉摸的惠更斯积分,实质上系一种精确解析光波传播的数学模型。其核心理念基于惠更斯原理——即每个波前面的点皆可视为新型波源,产生次级波。借助于对这些次级波进行积分运算,便能精准推算出光波在任意位置的强度分布情况。此法对于深入理解光的传播规律,特别是应对复杂光学系统的研究具有重要价值。

光线追迹的数值计算
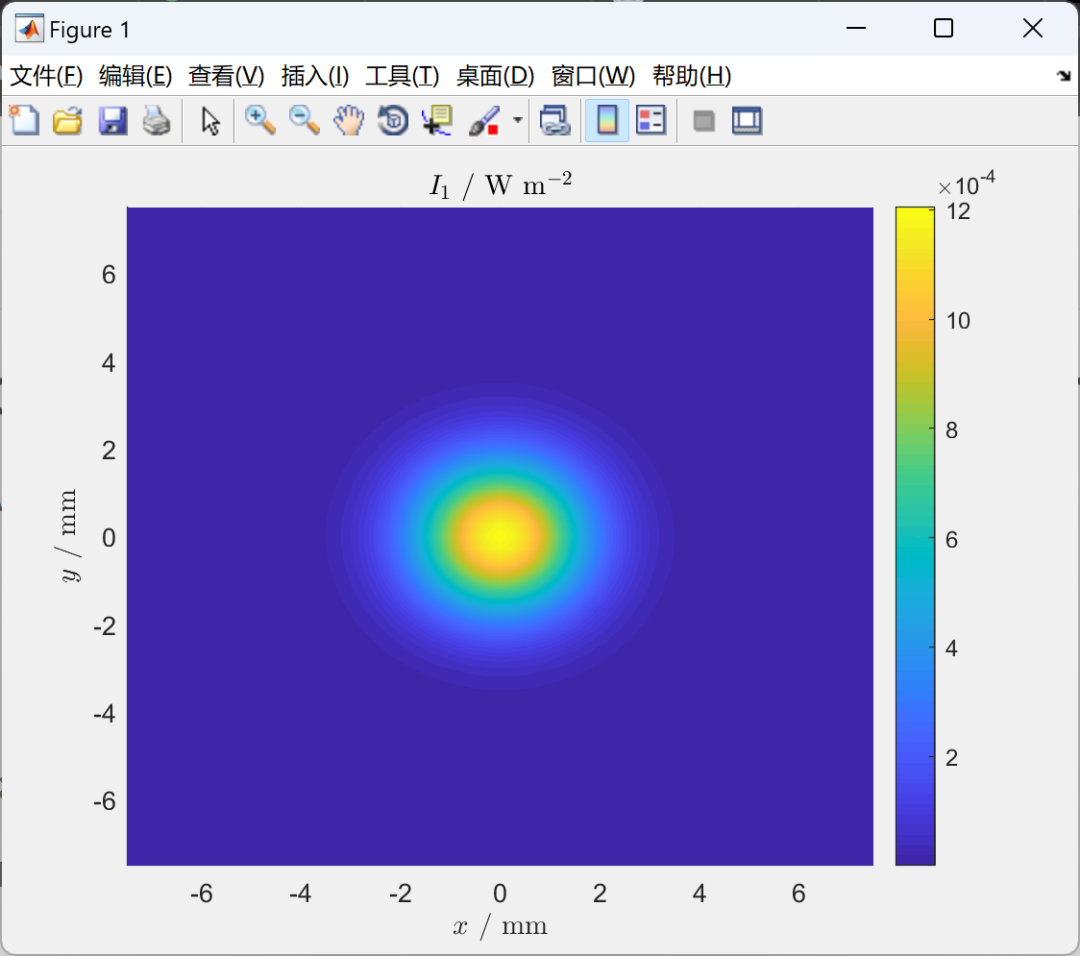
光线追迹作为看似科幻小说般的科技概念,实际是一种捕捉并模拟光线在光学设备内传播路线的方法。这种方法通过精密追踪每道光束的行进轨迹,能深入了解其在系统中的表现,具体涵盖如反射、折射及衍射等现象。借助此法,我们得以构建更为精细的光学系统模型,从而洞悉光线在其中的精确运动规律,进而提升测量精度。
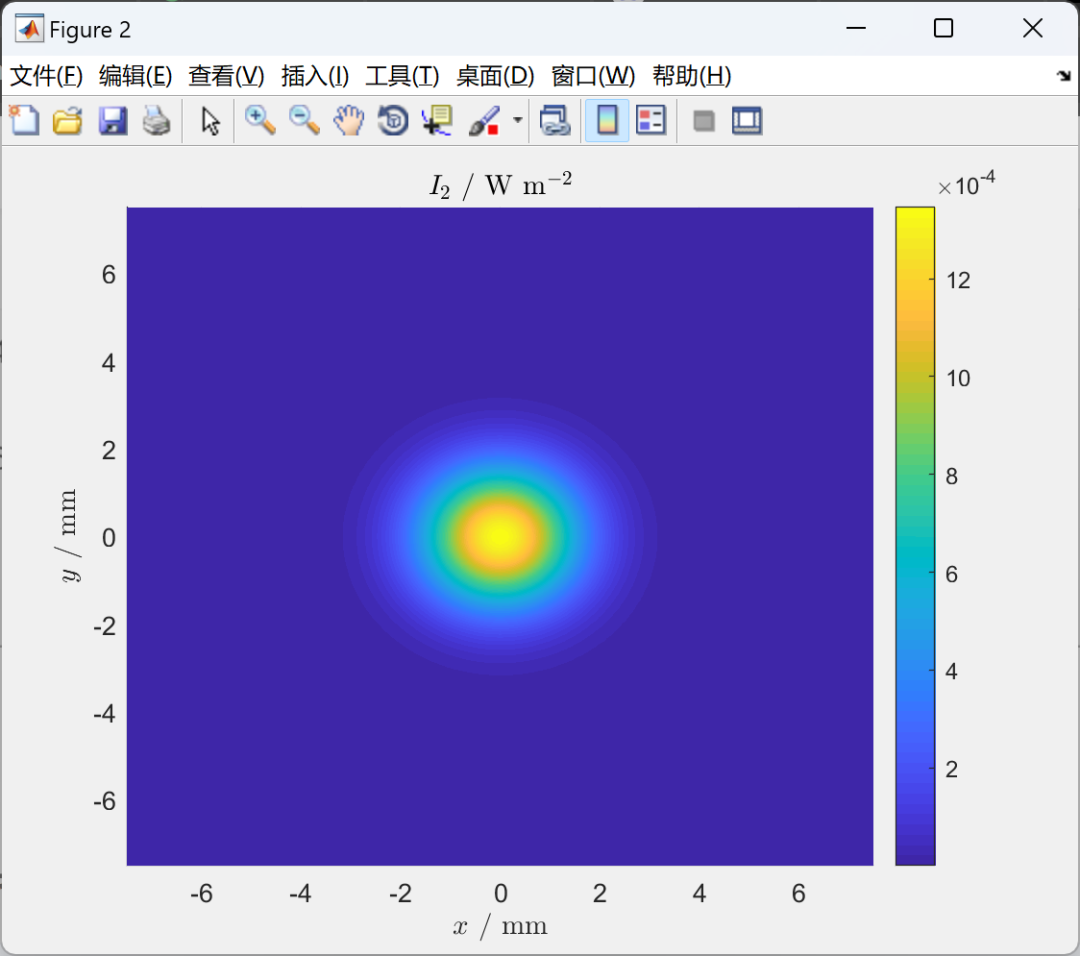
衍射校正的重新计算
科研人员先前已采用偏轴法对衍射效应对测量结果的影响加以修正。然而,随着精密度的日益提高,此方法逐渐显现不足。为此,我们重新演算并使用新颖方式提升修正之精确度。此过程犹如为精密测量设备进行精细调整,以确保其在亚纳米级别精度测量中的最佳表现。
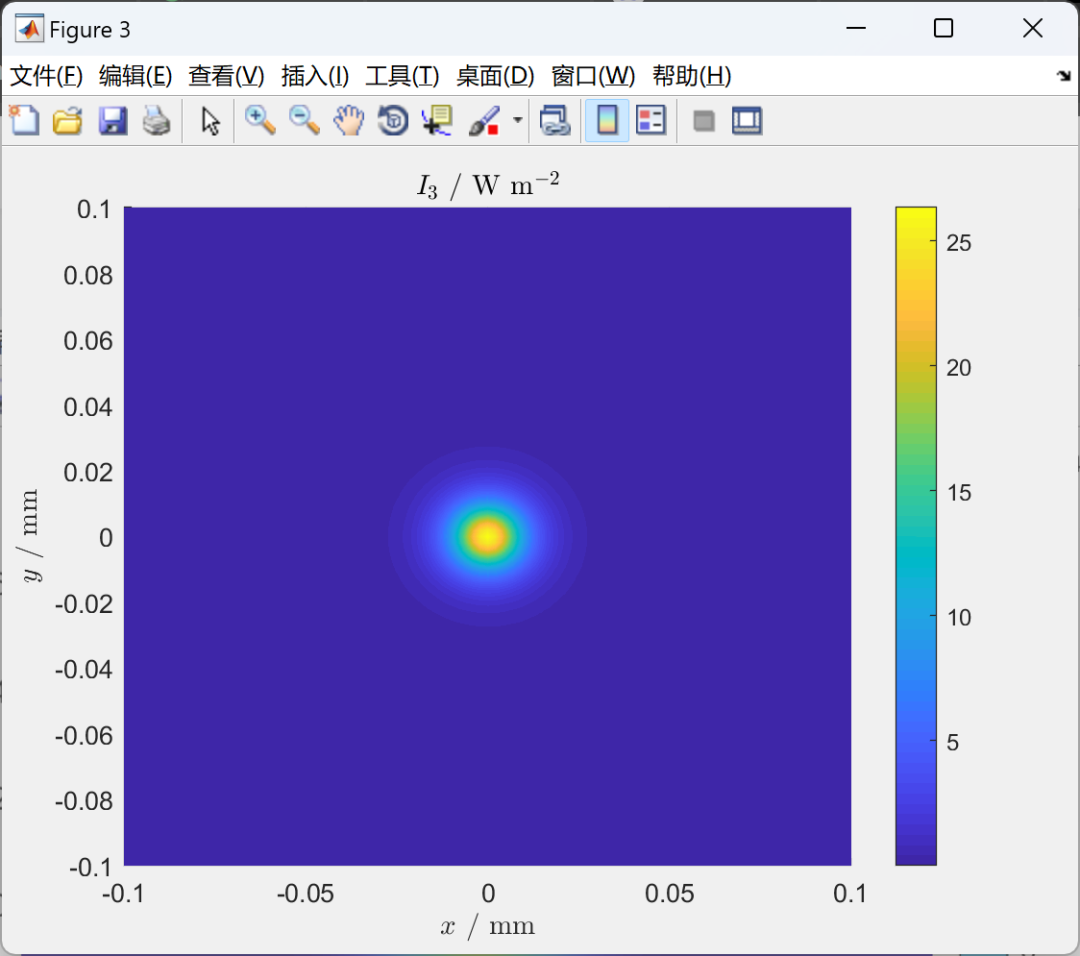
激光干涉测量的未来展望

凭藉科技不断创新之力,激光干涉测量正在步向高精度的新境界。新型精准的描述与校准方式的应用,使我们能更准确解释光线传播现象及更精确修正衍射效应所引发的误差。此举不仅推动了精密测量技术的进步,更为科研和工业生产开启了无限可能。
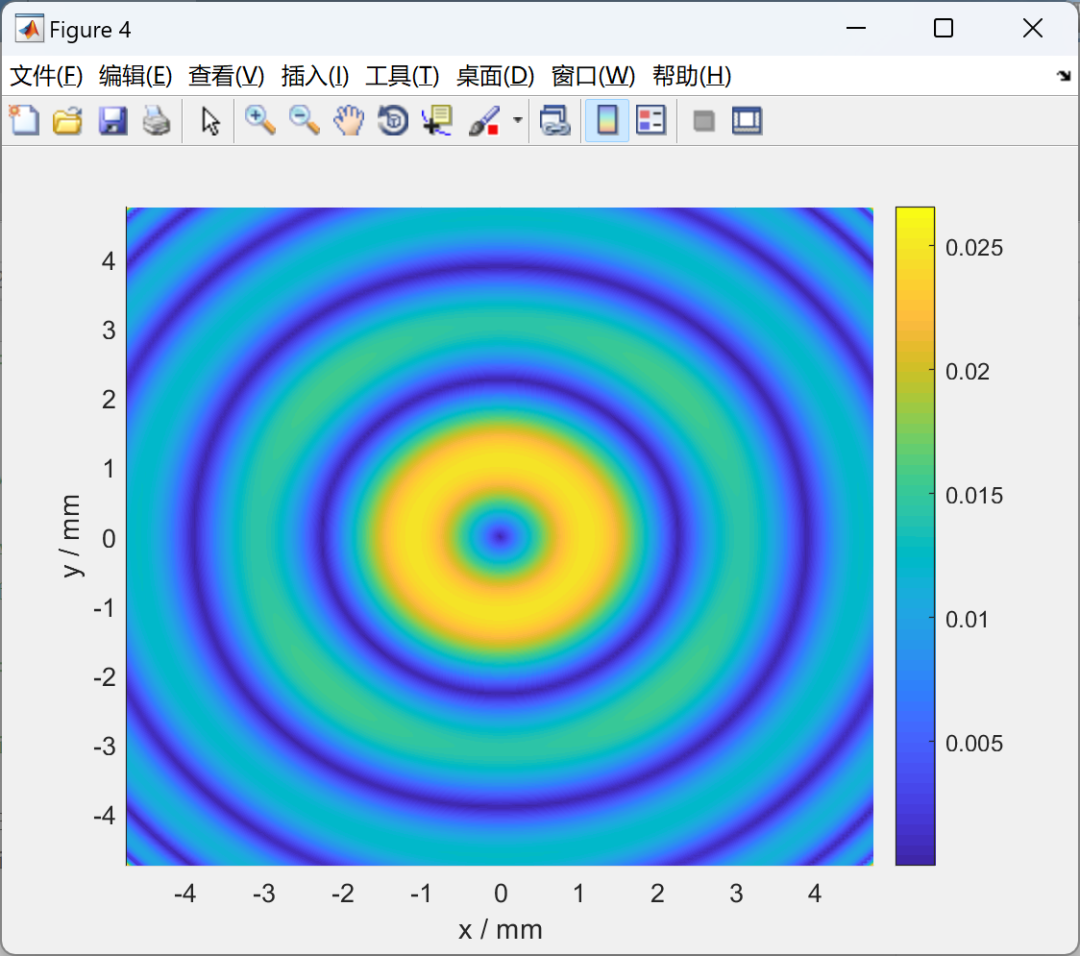
结语:精密测量的艺术与科学
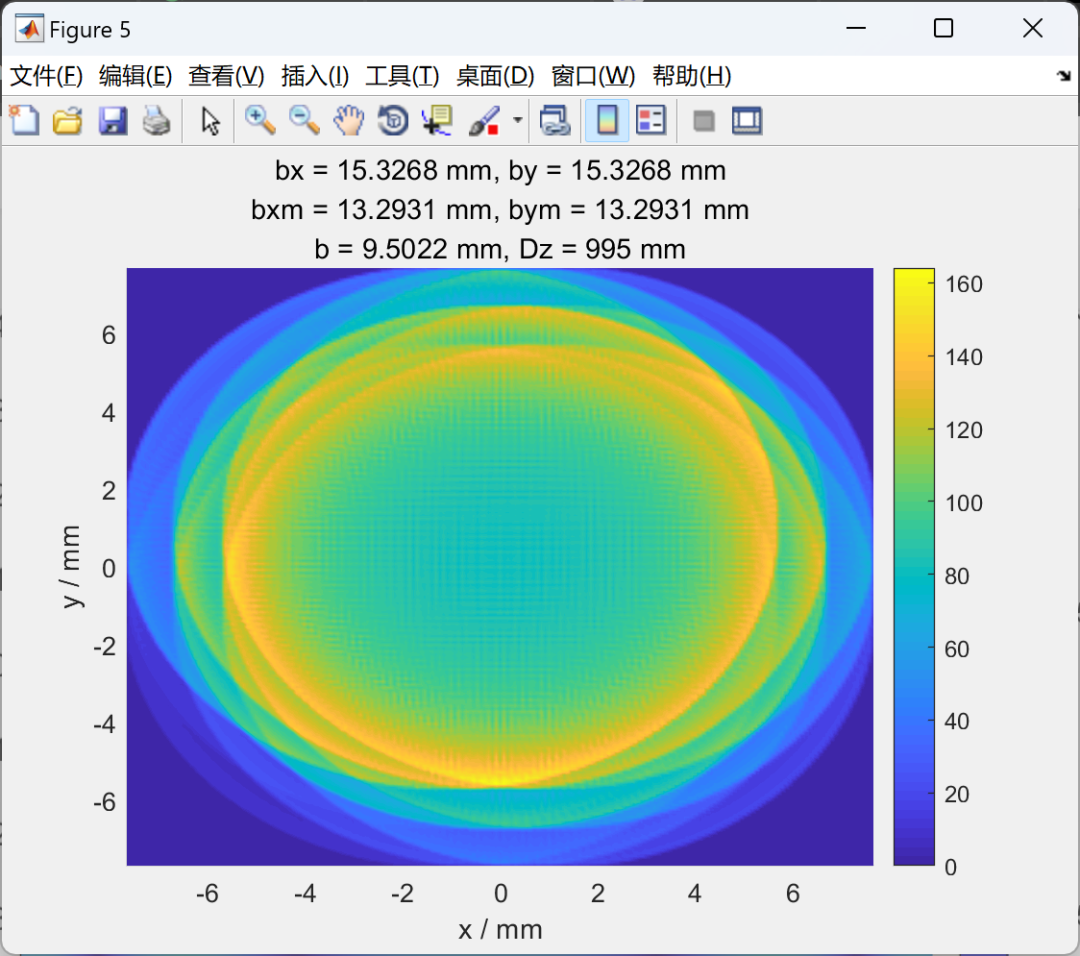
激光干涉测量作为精密测量学领域的艺术与科学,有力助推了人类探索未知的步伐。每次科技突破,犹如赠予科研人员的新钥匙,开启精确度更高的认知之门。此过程中,我们不仅掌握了更为精准的测量方法,也学会了应对挑战和思考创新。这不仅仅局限于技术层面的精益求精,更是对知识无尽探寻的执着追求。
在探寻微观领域之美的征程中,我们不禁发问:追求极限精度之路究竟还有多长?此问题或仅有光阴能给与解答。然而,可以确定的一点是,我们必将砥砺前行,持续探索,锐意创新,直至触达那看似遥不可及的亚纳米级精度。