
随着时间的推移,时序数据分析及精准预测在企业决策中日益重要。若能预知每日客流量走势,便可适时调整策略,规避风险,把握商机。本文将聚焦这一主题,以更深入、易懂的方式阐述运用Python实现以上目标的详尽步骤,特别注重强调如何准确识别异常数据。

一、时间序列数据的奥秘
先明确时间序列数据的概念,即按照特定时段或先后次序持续累计的数值集合。例如,线下零售店每日客流数据便是典型案例。此类数据对销售额具有直接影响,故深度分析与挖掘显得尤为关键。
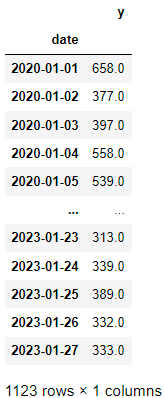
时序数据研究不仅考察数值的变迁,更须关注季节性、趋势及周期波动等多元因素,它们对理解研究结论具有关键意义。因此,严肃的时序分析必须重视并妥善考虑处理这类多元因素。
二、异常值检测的重要性
plt.figure(figsize=(10,4),dpi=100)
plt.plot(df)
plt.title("客流量趋势")
plt.show()
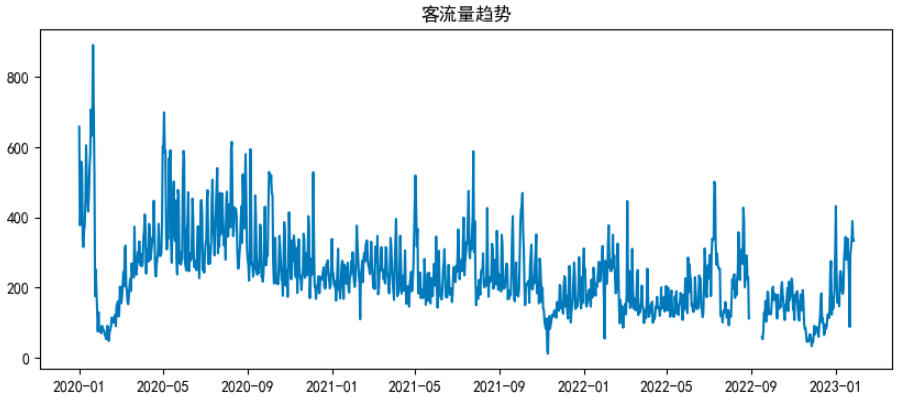
异常值即脱离大多数样本的个别数据点,这些偏差可能源于输入误差、测量误差或偶然事件等因素。因其对分析结果有重要影响,因此精准识别与去除至关重要。
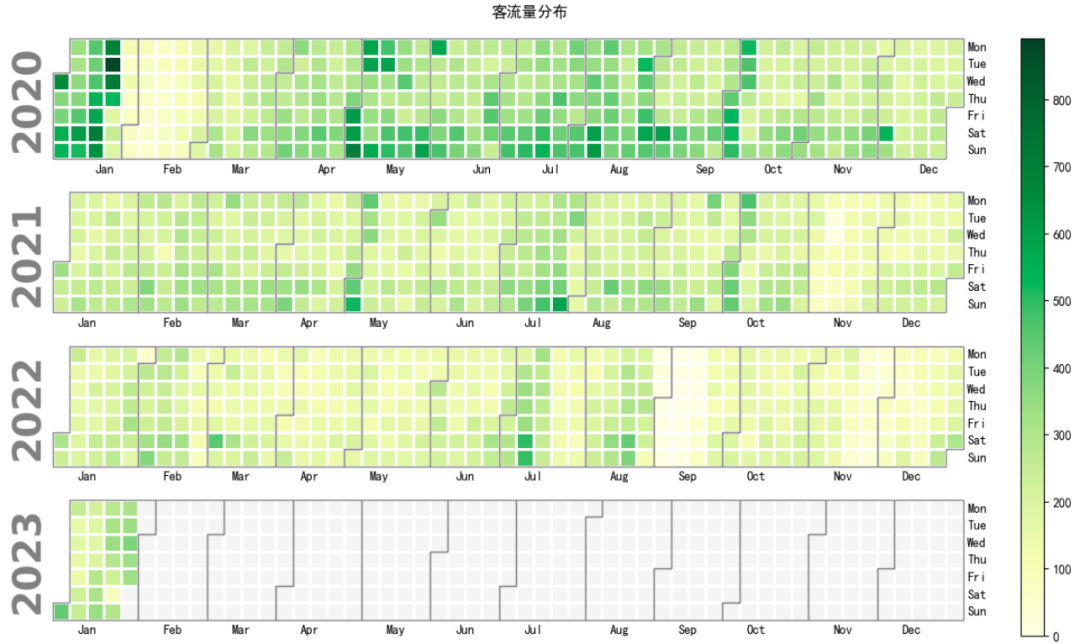
calplot.calplot(df.y,suptitle='客流量分布',cmap='YlGn');
若时序数据出现异常值(如某日客流量飙升至日常水平的十倍以上),将直接影响分析结果,甚至被误解为重要趋势,从而导致失败的决策。故而在进行时序数据分析之前,寻找并清除此类异常值至关重要。
三、单一维度异常值检测方法
在时序数据分析领域,常采用三类异常值检测手段:3σ法则、Z-score法及盒线图法(Box)。它们均基于数据数值进行异常判断,虽简便实用,却存在一定局限性。
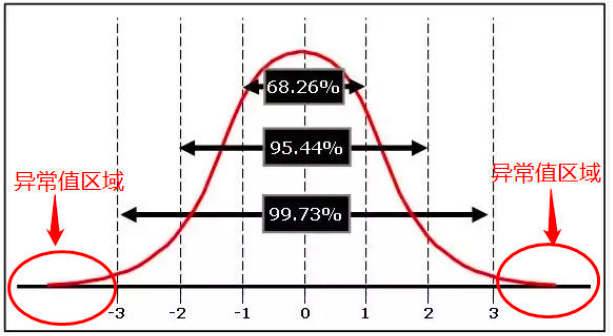
基于正态分布假定,sigma方法直接将超出三倍标准差之外的数值划入异常范围,这一过程简便易行;而z-score法则则是通过计算数据偏离均值的程度来设定异常值界限,同样需要正态分布假定作为前提条件。另一方面,箱线图(BoxPlot)则依据数据的四分位距来识别异常值,无需正态分布假定,然而它仅能从一个方向上检测出异常现象。
四、多维度异常值检测法的优势
# 3sigma
def three_sigma(df):
mean=df.y.mean()
std=df.y.std()
upper_limit=mean+3*std
lower_limit=mean-3*std
df['anomaly']=df.y.apply(lambda x: 1 if (x>upper_limit )
or (x<lower_limit) else 0)
return df
df1 = three_sigma(df.copy())
df1[df1.anomaly==1]
与常规单一统计方法相比,多元化评估方法能更精确而敏锐地捕捉数据中的异变。此法通过全方位探讨数据规律,审慎评定,从而提高突变值判定的确切性。例如,对时间序列数据,还可细分至年、月、日、周、季等时间维度,深化剖析,再度加强离群值辨识度。
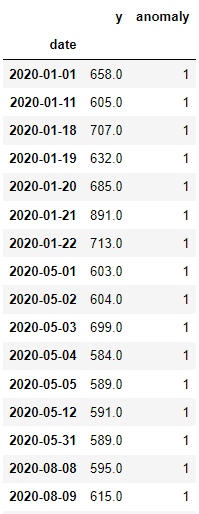
在对单维数据进行分析时,可能会忽略重要资讯。例如,节假日旅客量骤增可能误认为是数据收集出现误差。但当结合多种关联性分析与特定日期特性因素对比后,便能精确检测到异常状况。
fig, ax = plt.subplots(figsize=(10,4))
a = df1.loc[df1['anomaly'] == 1, ['y']] #anomaly
ax.plot(df.index, df['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
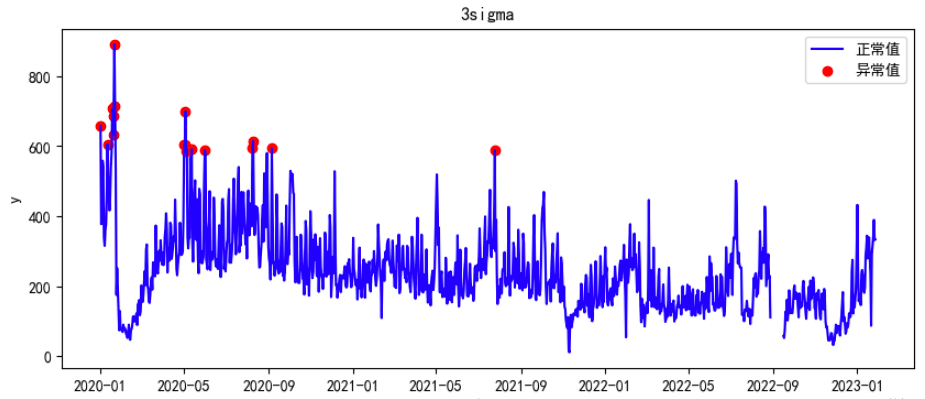
plt.title(f'3sigma')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();
五、PyOD:多维度异常值检测的利器
在多维异常监测技术领域,PyOD作为一款尖端智能算法库,专门从事异常值识别工作,深度分析海量数据,实现了对各类异常值的精准识别。借助PyOD的卓越性能,我们能够从时间序列中提取出年度、月份、日期乃至星期和季节等多种特征类别。
强势武器PyOD作为强有力的多元大数据分析助手,凭借深刻解读与分析数据的实力,使得异常值发现精度得到显著提高。此外,该工具还具备丰富多样的异常值检测算法,以满足实际应用中的广泛需求。
六、Pycaret:让异常值检测更简单

若体感PyOD较为复杂,不妨尝试使用Python版的Pycaret自动化机器智能助手,简化离群点参数调整步骤,有助提升工作效率与准确性,让相关任务执行更为从容。
# Z-Score
def z_score(df,threshold):
mean=df.y.mean()
std=df.y.std()
df['z_score']=df.y.apply(lambda x:abs(x-mean)/std)
df['anomaly']=df.z_score.apply(lambda x: 1 if x>threshold else 0)
return df
#设置阈值为2或3,当阈值为3时便相当于3sigma
threshold=2
df2 = z_score(df.copy(),threshold)
df2[df2.anomaly==1]
利用想象力与Pycaret技术,可预期实现:自动执行异常值检测工具能用简单而经济的方式大幅节约资源。Pycaret作为关键环节,提供精确高效的检测功能,助推我们完成此项任务。同时,Pycaret为广大用户供应多元化的异常值检测算法,充分满足多样化需求。
七、实战演练:如何使用Pycaret进行异常值检测
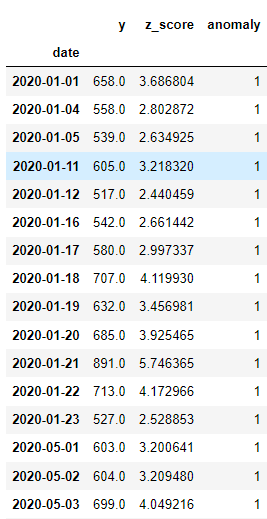
在实战环境中应用Pycaret进行异常值识别时,我们需要对含有日期类型字段的内容深挖。首先,将其转化成包含年份、月分、日期、星期以及季度等时间要素在内的“特征”;然后,借助Pycaret提供的特性模型anomaly建立与预测新数据集相应的数学模型。
fig, ax = plt.subplots(figsize=(10,4))
a = df2.loc[df2['anomaly'] == 1, ['y']]
ax.plot(df.index, df['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
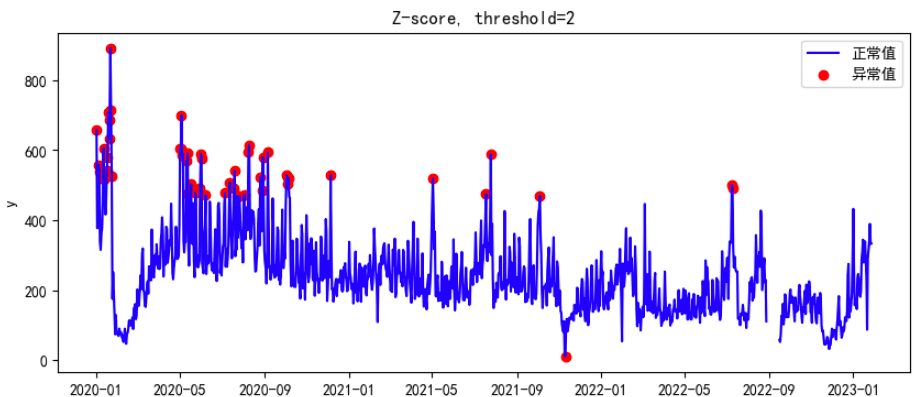
plt.title(f'Z-score, {threshold=}')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();
八、异常值检测的挑战与未来
尽管异常值检测法琳琅满目,但每种方法皆有其局限性。例如,3σ法则、Z-Score以及Box等传统方法往往仅从单一数据维度识别异常点,难免有所疏忽。相较而言,多维异常值检测法凭借深度挖掘与精准把握各数据特征的独特优势,更具科学严谨性。
九、总结与展望
您可有过因异常值检测而困惑不已的经历?我们愿意倾听并一起探讨对策,期待您能在评论中抒发见解。期望这篇文章能够为您带来思路,期待您的宝贵回馈与分享!
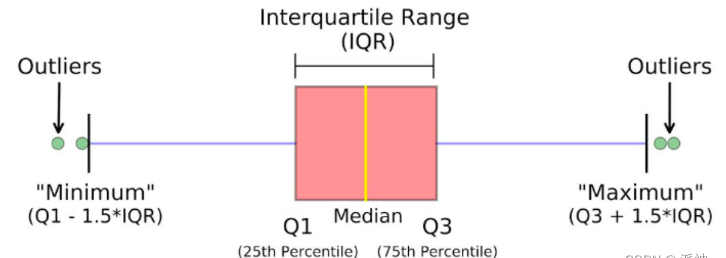
def box_plot(df):
q1=np.nanpercentile(df.y,25)
q3=np.nanpercentile(df.y,75)
iqr=q3-q1
lower_limit=q1-1.5*iqr
upper_limit=q3+1.5*iqr
df['anomaly']=df.y.apply(lambda x: 1 if x<lower_limit or x>upper_limit
else 0)
return df
df3 = box_plot(df.copy())
df3[df3.anomaly==1]