在生活常识中,地球看似球状完美,然而实则具有复杂无序的形态。为了精确描绘这个独特的外形,科学家采用了一种名为“参考椭球体”的数学方式。这个椭球体不仅可帮助我们对地球外形进行精准模拟,更是构建了一套科学统一的定位坐标系以供精准的位置描述和度量。因此,在地理测量中,大地水准面与参考椭球体的高程差为不可忽略的关键要素。本文旨在深度解读这二者的密切联系及其在地理信息系统中的实际运用。
1.参考椭球体的定义与重要性
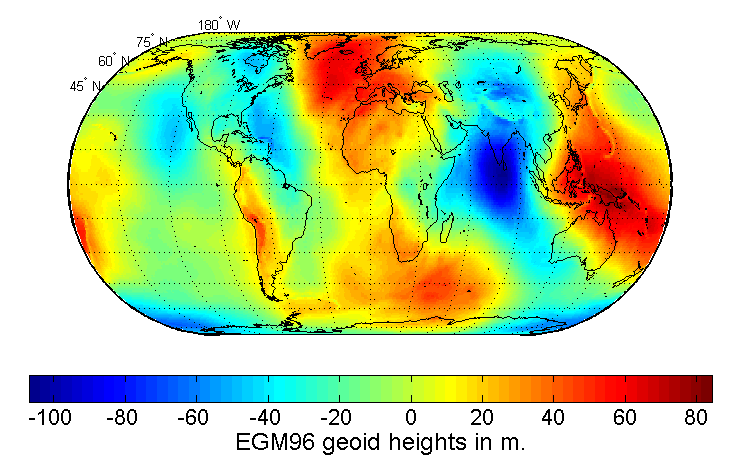
参考椭球体作为一种拟合现实地球的理想化数学模型,它采用单一几何形状模拟了不规则的地球表面。借助于此模型,人类得以在全球化范围内进行精确度较高的空间定位和测量,同时也为地理信息系统的发展提供了坚实的理论基础。试想,若无参考椭球体,空间位置的描述将变得极其繁琐,甚至可能导致同一地点出现多种不同的坐标表述情况。
选取适宜的参考椭球体,对地理计量领域至关重要。为迎合各地起伏的地势,人们常依据情况选用各自的椭球体。因此,参考椭球体的多样性使我们得以在全球范围内精确测量,并为各国地理信息系统奠定基石。无论在城市规划、交通管理,抑或自然资源的开发与保护方面,参考椭球体均扮演着无可替代的角色。
2.大地水准面与参考椭球体的高度差异
大地水准面乃是海平面在静止状态下的全球平均水平面,是反映地球引力场的重要物理量。虽然其概念与参考椭球体有别,后者仅为一种物理模型,但二者之间的高度差,即大地水准面起伏,所蕴含的并非仅仅数值概念,更涉及到地球内部结构、地壳活动和水域流动等复杂的自然作用过程。
对大地水准面与参照椭球体间高度偏差的掌握不仅对科研事业、更对工程实践具有核心重要性。例如,精准测量对水资源管控有极大推进作用,进而实现优化的水利策略。同时,在地震监测及灾害预警领域,理解地表与椭球体的关联性亦可为我们提供关键的参考信息,助力我们更有效地抵御自然灾害。
3.坐标系统的统一与测量精度
结合参考椭球体所构建的几何模型,可以确立统一的坐标系统,使得位置描述及测量更为便捷。在同一坐标系中,不同地点的坐标数值具有可比性,测量成果亦具一致性。此种统一性对地图绘制、导航系统乃至各类地理信息应用均至关重要。
需要明确指出,全球各地的测量体系众多且各具特色。例如,北美采用NAD83基准,欧洲则为ETRS89基准,而世界通用的WGS84基准也广受欢迎。这些基准间的微小差异都可能对测量精确度产生影响。因此,在跨地区测量及数据共享过程中,我们需充分理解并掌握各种坐标系统,以免因坐标不统一引发数据误差。
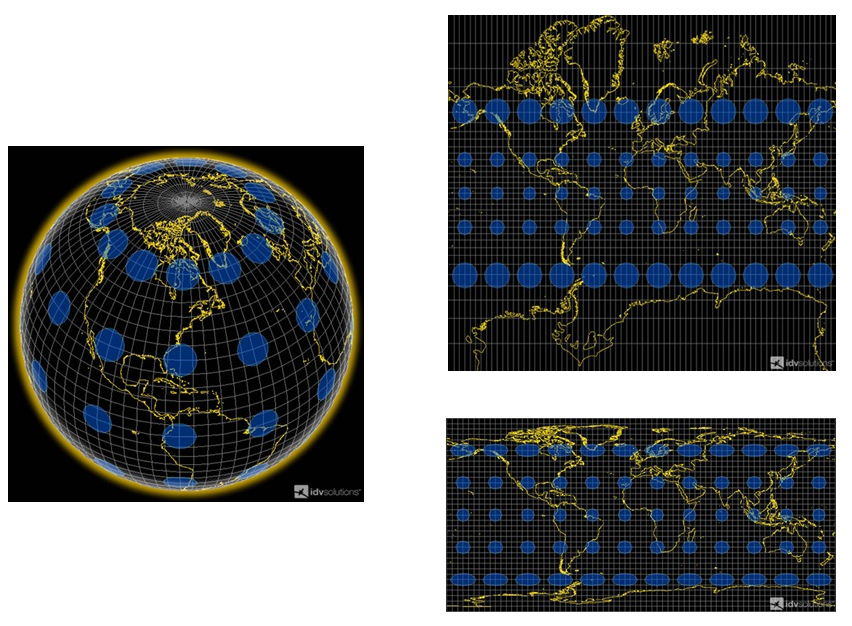
4.地理坐标系的三维与二维转换
地理坐标系统拥有三维特性,然而为了在地图书籍及屏幕上展示,我们需要转译成二维形式。此过程即为投影(MapProjection)。常用的投影方法包括等距矩形投影(PlatteCarre)与墨卡托投影(Mercator)。每种投影方式皆具备独特优势与劣势,因此选择适当的投影方式对地图的易读性以及信息传递具有关键作用。
譬如,尽管PLATTECARRE投影不适用于航海等领域,但凭借其简单明确的坐标与像素映射,被广泛采用为许多GIS软件的默认投影方式。至于墨卡托投影,其图形直观性优于前者,然而在极地地域使用时容易产生误差。因此,投影法的选择对地图美观度以及实用价值有着深刻影响。
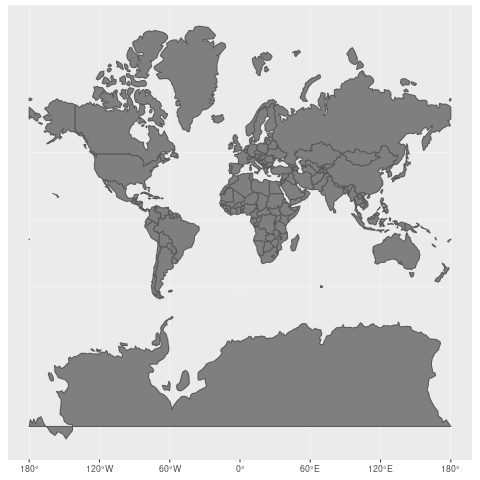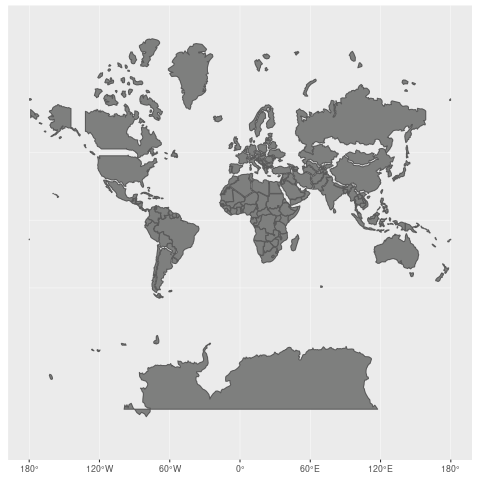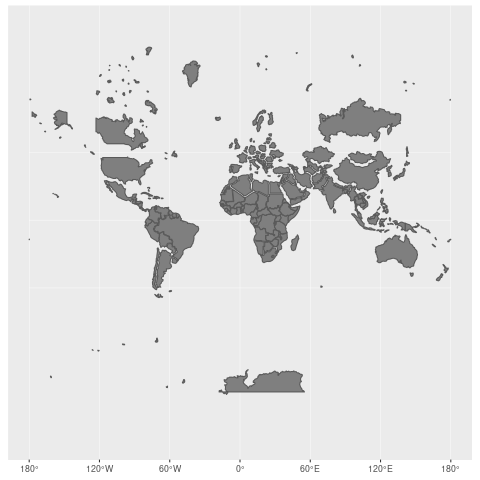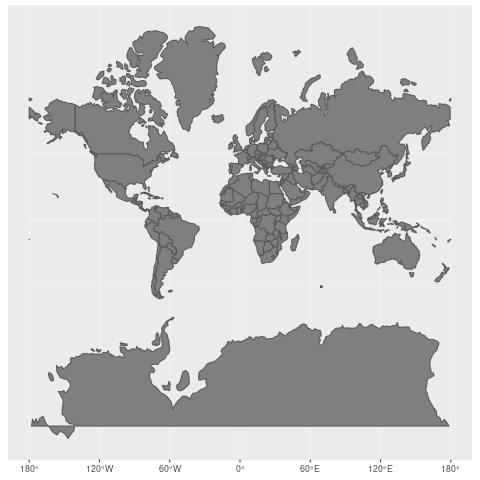
5.数据存储与显示的最佳实践
在地理信息应用中,数据普遍存储于WGS84坐标系统,展现时转换至伪墨卡托投影。此方式既保证了数据精度,又提升了展示效果。尽管伪墨卡托投影在极地地区存在一定程度的变形,但其带来的更佳视觉感受和易懂性使之成为理想选择。
同期,协助我们精准实现地理信息应用是映射API的便捷应用。它能以经纬度(EPSG:4326)输入,规划转化为谷歌地图标准“Web墨卡托”(EPSG:3857)坐标系输出。这一智能化制图过程,极大提高了用户使用便利性,同时也简化了地理数据应用流程。