数据领域中,异常数值与常规数值界限清晰。异常数值犹如融入普通队伍中的特殊个体,与多数数值相去甚远,而常规数值则构成了整齐划一的大多数。这两者的存在以及如何识别异常数值,构成了数据处理领域的一个既关键又充满趣味的问题。
异常值与正常值的界定
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as st
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')df=pdf.read_excel("scrap_data.xlsx", skiprows=2)
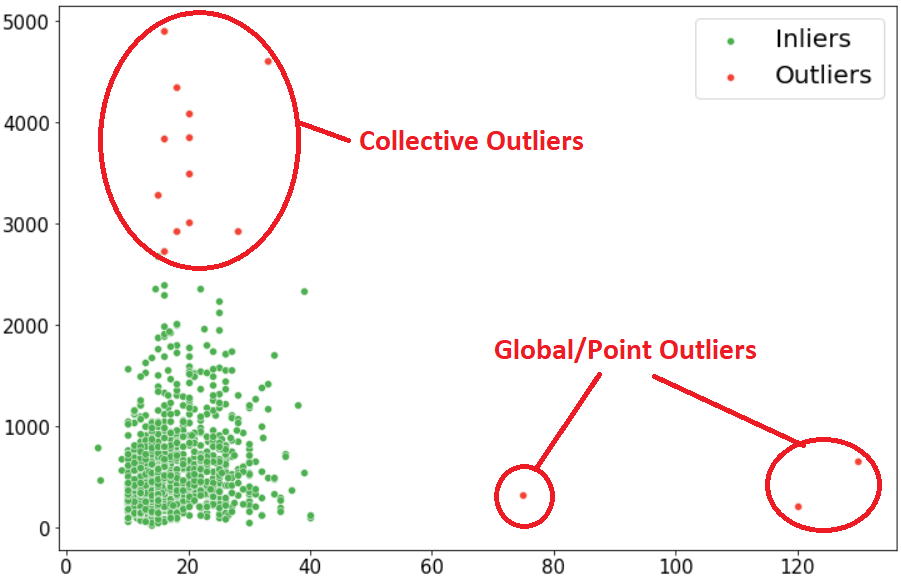
df.head(), print('shape of data:',df.shape)数据集中,异常值显得格外突出,它们与多数数据相异,而常规数据则占据了数据集的大部分。比如,在一份学生成绩数据集中,大部分成绩都集中在某一区间,但偶尔会出现一些极低或极高的分数,这些分数即为异常值。这就像在众多身高正常的人中,突然出现一个特别高或特别矮的人。正确地区分这两种数据对于数据的精确分析至关重要。在许多情况下,函数能帮助我们处理数据,识别这些值。例如,通过构建函数来计算四分位数范围,我们能在复杂的数据集中更精确地识别出异常值。
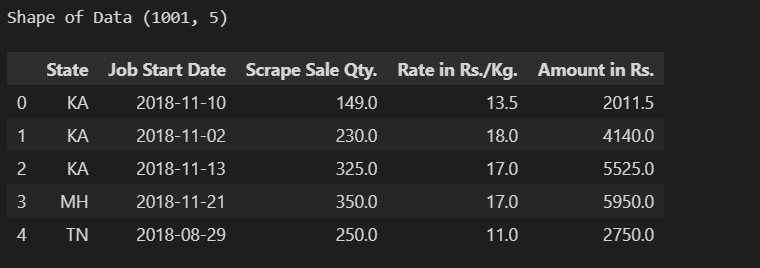
plt.figure(figsize =(15,5))
plt.subplot(1,2,1)
sns.lineplot(x=df['Job Start Date'], y=df['Rate in Rs./Kg.'], color='r')
plt.title("Steel Scrap Rate (Rs/Kg)", fontsize=20)
plt.xlabel('Date')
plt.subplot(1,2,2)
sns.lineplot(x=df['Job Start Date'], y=df['Scrape Sale Qty.'], color='b')
plt.title("Steel Scrap Weight (Rs/Kg)", fontsize=20)
plt.xlabel('Date')数据集的评估结果会受到异常值有无的影响。比如,在市场调研时,如果产品成交价中出现异常的高价或低价,这会干扰我们对市场平均价格的准确判断。因此,无论是进行理论研究还是商业应用,对异常值和正常值进行明确区分,都是进行后续数据处理的前提。
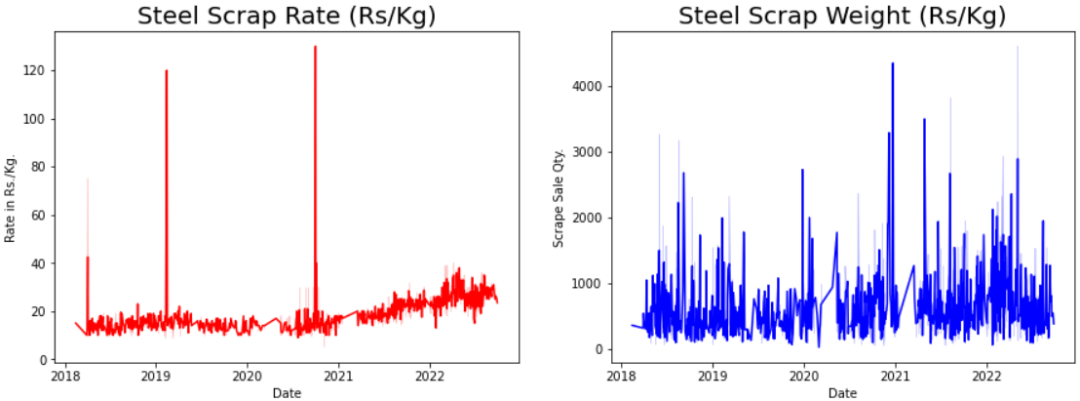
全局或点异常值检测
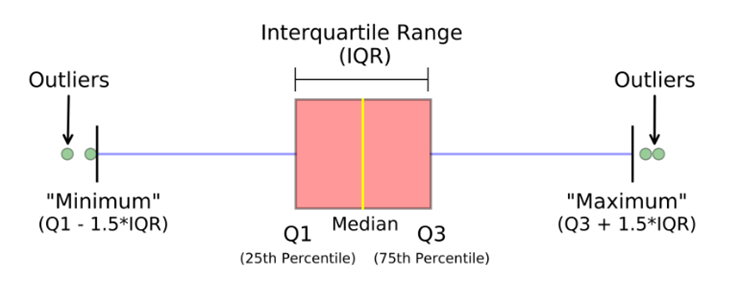
异常值检测的多数方法主要关注的是单个数据点或是整个数据集的异常情况,即那些显著偏离整体分布的数据。以某地区每日气温为例,若某日气温异常偏高或偏低,与日常气温数据相差较大,那么这一数据点便构成了全局异常值。在此过程中,计算工具扮演着关键角色。我们能够迅速计算出四分位距(IQR),它将数据集分成四个等份,以此方法来衡量数据的波动性。
plt.figure(figsize=(15,5))
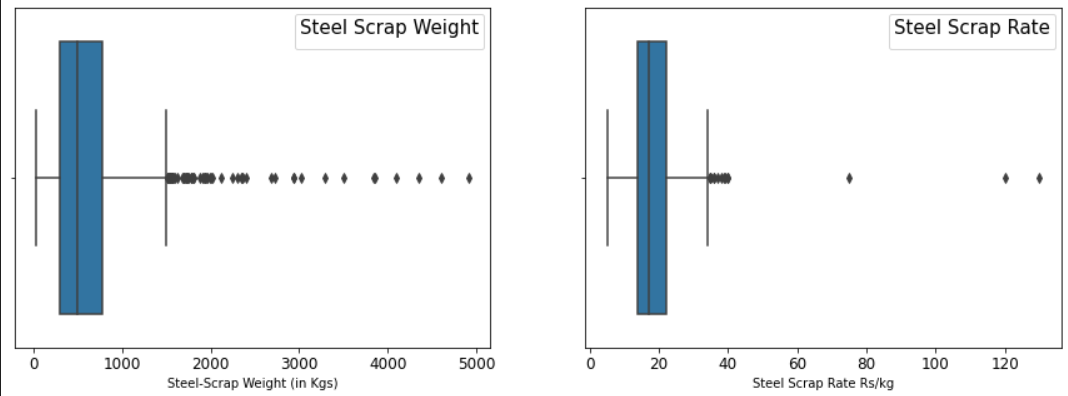
plt.subplot(1,2,1)sns.boxplot(df['Scrape Sale Qty.'])
plt.xticks(fontsize = (12))
plt.xlabel('Steel-Scrap Weight (in Kgs)')
plt.legend (title="Steel Scrap Weight", fontsize=10, title_fontsize=15)使用IQR需进行特定步骤,比如设定一个上下限,一旦数据点越界,便视为异常。此外,Z分数也颇有效,若数据点的Z分数低于-3或超过+3,则可能被视为异常。社科研究中,将素材转化为数据后,Z分数能迅速帮我们挑出不符常规研究结论的数据,即异常值。
Z分数的运用
def identifying_treating_outliers(df,col,remove_or_fill_with_quartile):
q1=df[col].quantile(0.25)
q3=df[col].quantile(0.75)
iqr=q3-q1
lower_fence=q1-1.5*(iqr)
upper_fence=q3+1.5*(iqr)
print('Lower Fence;', lower_fence)
print('Upper Fence:', upper_fence)
print('Total number of outliers are left:', df[df[col] upper_fence].shape[0])
if remove_or_fill_with_quartile=="drop":
df.drop(df.loc[df[col]upper_fence].index,inplace=True)
elif remove_or_fill_with_quartile=="fill":
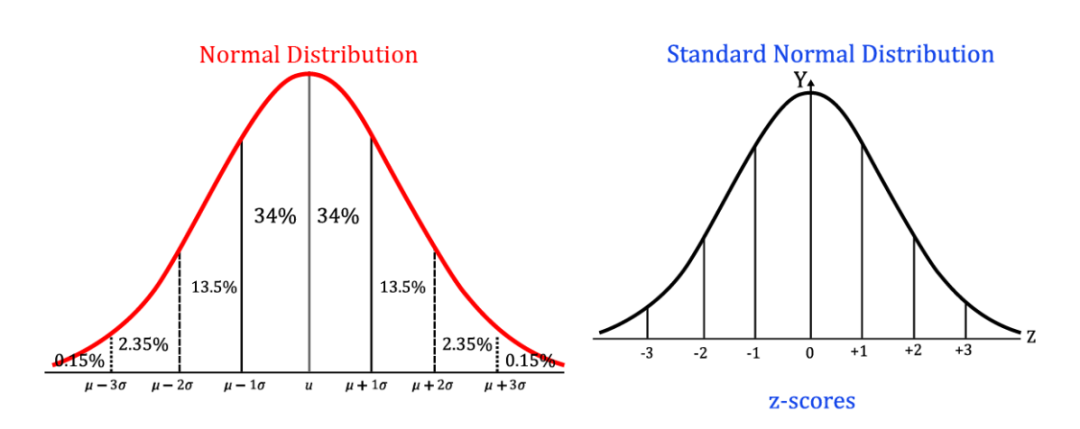
df[col] = np.where(df[col] upper_fence, upper_fence, df[col])Z分数能帮助我们用数字来找出数据中的特殊值。它能将数据调整成符合标准正态分布的形式。这就像把不同单位换算成统一的度量标准。一旦有了这个统一标准,我们就能轻松地对比不同数据间的差异。比如,在分析人体身高和体重数据时,将它们转换成Z分数后,比较起来就简单多了。我们能清楚地看到哪些数据点在整体分布中显得特别突出。
identifying_treating_outliers(df,'Scrape Sale Qty.','drop')
identifying_treating_outliers(df,'Rate in Rs./Kg.','drop')只需几行代码便可计算出Z分数,同时分布图也能直观展示转换前后的变化。以金融产品收益数据集为例,运用Z分数后,我们可以直接识别出异常收益值,从而辅助我们评估投资风险。然而,Z分数并非无所不能,在处理多变量大数据时,其应用也会遇到困难。
plt.figure(figsize=(15,5))LocalOutlierFinder
plt.subplot(1,2,1)
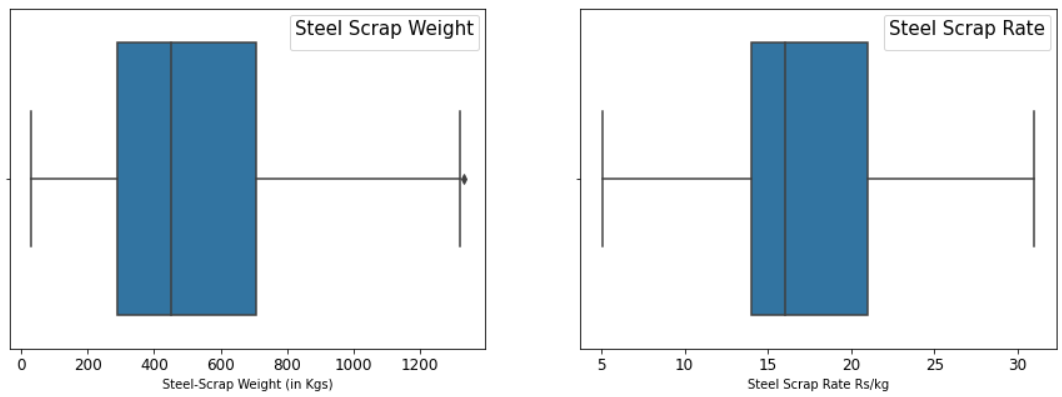
sns.boxplot(df['Scrape Sale Qty.'])
plt.xticks(fontsize = (12))
plt.xlabel('Steel-Scrap Weight (in Kgs)')
plt.legend (title="Steel Scrap Weight", fontsize=10, title_fontsize=15)本地异常值检测器,这是一种无需监督的机器学习工具。它通过分析数据点周围的邻近区域密度来识别异常值。当数据集中不同区域的分布密度存在差异时,这种技术尤为有效。就好比在一个由多种植物群落构成的生态系统中,若某一区域的植物密度与整体特征不符,就可能存在异常情况。
plt.subplot(1,2,2)
sns.boxplot(df['Rate in Rs./Kg.'])
plt.xlabel('Steel Scrap Rate Rs/kg')
plt.xticks(fontsize =(12));
plt.legend (title="Steel Scrap Rate", fontsize=10, title_fontsize=15);这项技术存在一定的限制。比如在我之前的研究中,当我把污染模式设置为“自动”时,发现其表现并不出色。这是因为我的数据密度变化不大,在此条件下,它无法有效检测出异常值。因此,在实际应用中,需根据不同数据集的特点来挑选恰当的异常值检测策略。
DBSCAN技术
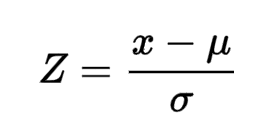
DBSCAN算法通过设置Min_samples和Epsilon两个关键参数,与邻近数据点建立集群,以此来识别正常数据和异常数据。Epsilon代表一个半径区域,Min_samples则是指在这个区域内需要考虑的数据点数。这往往需要依赖专业经验或领域知识。比如在图像处理领域,若要检查图像中某特定物体周围的数据点是否正常,DBSCAN技术便能派上用场。
操作时需根据数据特性挑选恰当的参数。在我的研究里,由于特征数不超过五个,我选取了两个关键数字特征来学习和展示。选定了恰当的Epsilon和Min_samples值后,DBSCAN便能高效识别出明显的异常值,这对我们处理真实数据极为有益。
多种方法的比较与实践
文中提到了四种在数据集中识别异常值的技术,这些方法在多个实际数据集上均进行了应用,并呈现了各自的效果。不同领域和具体数据集的特点使得每种技术都有其适用性和局限性。以处理包含大量变量的大数据集为例,IQR、Z分数或LocalOutlierFinder可能不太适用,而DBSCAN则可能更为适宜。
# Applying Zscore in Scrap Rate column defining dataframe by dfn
zr = st.zscore(df['Rate in Rs./Kg.'])
dfn = df[(zr-3)]
# Applying Zscore in Steel Weight Column defining dataframe by dfnf
zw= st.zscore(dfn['Scrape Sale Qty.'])
dfnf = dfn[(zw-3)]工作中或研究时,若需进行数据中的异常值查找,您会挑选何种手段?期待大家能点赞、转发这篇文章,亦或是在评论区展开交流。
plt.figure(figsize=(12,5))