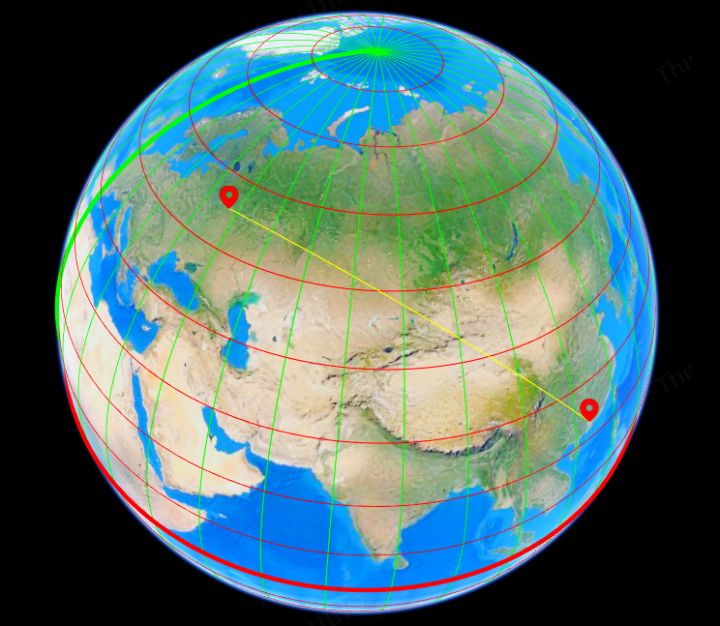
经纬度如同开启地球表面的神秘“钥匙”。它能精确定位地球上的每一个点。然而,在纸质地图盛行的年代,为了在平面上展现这个圆球形的地球,我们不得不使用投影技术。这一过程中,蕴含了众多令人称奇的奥秘。
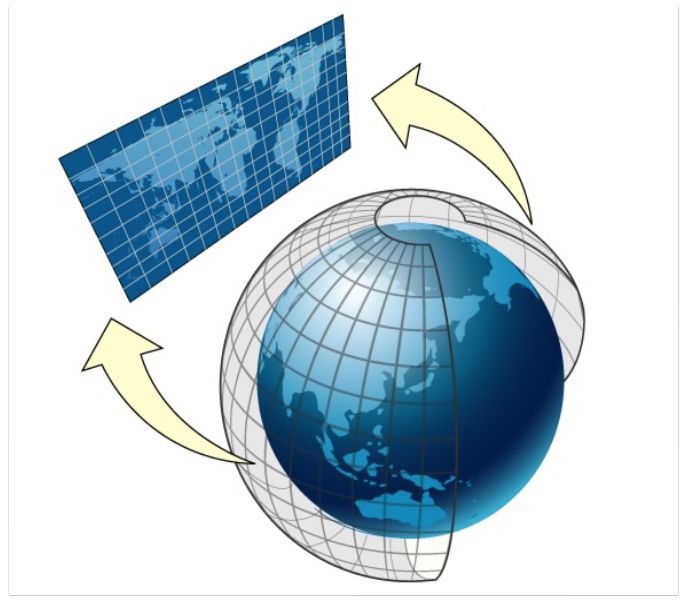
从地球到平面的转化
地球形状接近椭圆,通过经纬度来标示其在球面上的具体位置。过去,纸质地图盛行,绘制地图时必须使用投影方法。比如,在制作城市地图集时,制图者需设法将地形展现在平面上。这不仅关乎地图的美观,更是测量工作的基础。经过投影,采用直角坐标系后,坐标变得易于进行各种测量和计算,例如建筑测量人员据此确定建筑之间的距离等。这种转换是地图发展的必然趋势,将立体的地球转化为平面图,从而改变了我们对世界的认知方式。
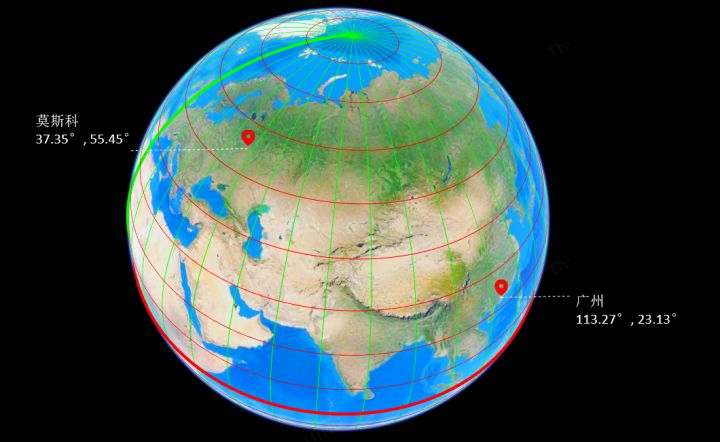
大圆距离的计算
计算两地间的距离,常采用Haversine公式。这在航运等行业中尤为关键。例如,货轮从广州驶向悉尼,船员会依据经纬度来规划出最节省成本的航线。一旦确定了两个点的经纬度,就可以利用公式计算出两点间的最短距离,即大圆距离。这样的计算使人们对地理距离有了更精确的认识。在当前贸易运输的背景下,这一理论对构建更为高效的全球物流网络具有重要意义。
Web墨卡托投影
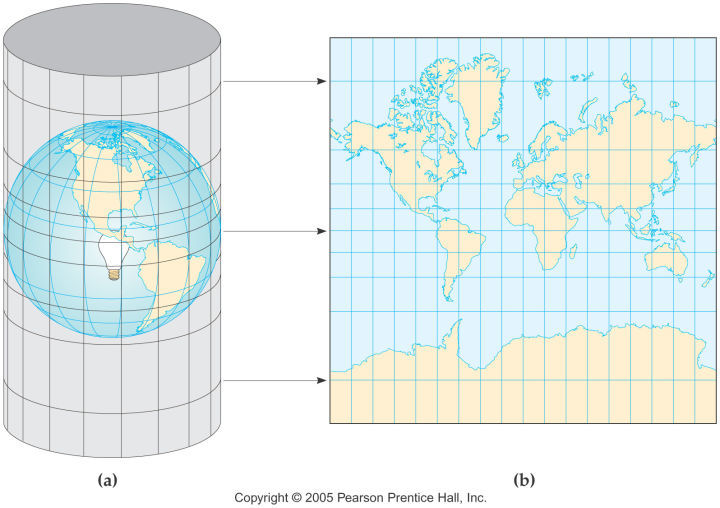
在此类应用中,Web墨卡托投影非常普遍。其原理类似一款游戏,设想地球被一个圆柱包裹,圆柱与赤道相切,中心有一盏灯将地球图案投射到圆柱上,然后展开。这种投影简化了椭球体,将其转化为正球体,并使用特定的半轴长度。例如,在绘制全球网络地图时,就会使用这种投影。它将世界呈现为一个正方形,便于切片等操作。
投影的范围限制与弊端
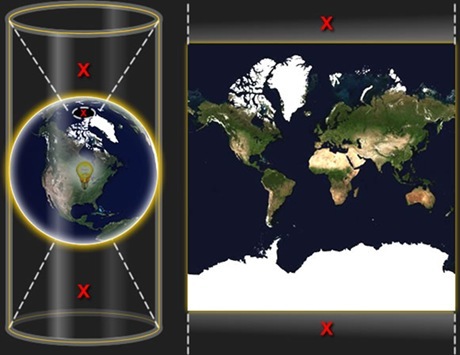
墨卡托圆柱投影在两极附近会有局限性。在接近两极的纬度上,Y坐标会趋向无穷大,这给地图绘制带来了挑战。因此,我们通常会对纬度进行限制,以便将世界地图贴合在一个正方形区域内。但这种简化后的球体并非严格等角。在绘制极地地区的科学考察地图时,我们必须考虑到这种非等角投影可能带来的误差,因为它可能会影响到测量的准确性或地图上形状的展示。
投影后的角度与形状关系
在墨卡托投影的图面上,有个现象挺有意思,就是图面上的方向线夹角和球面上的相应夹角是一样的。这就像用放大镜看图案,图案虽然放大了,但形状没变。当我们用这种投影法来绘制苔原地区的生态分布图时,可以看到生物群落的形状非常精确,但面积却发生了扭曲,而且越往高纬度,这种扭曲就越明显。
投影的取舍与平衡

地图投影无法完美兼顾等角和等积的特性。在制作政治区域划分图时,人们可能更看重等积;而在绘制地形地貌图时,等角可能更为重要。实际情况中,我们需根据具体需求来挑选。例如,地质学家研究板块分布时,并不需要过分关注面积是否相等。亲爱的读者,在日常生活中,你是否思考过这些地图投影背后的知识?欢迎点赞和分享这篇文章。