地图投影在地理信息领域扮演关键角色,然而,其中的众多繁复计算和理论,往往让人感到困扰。
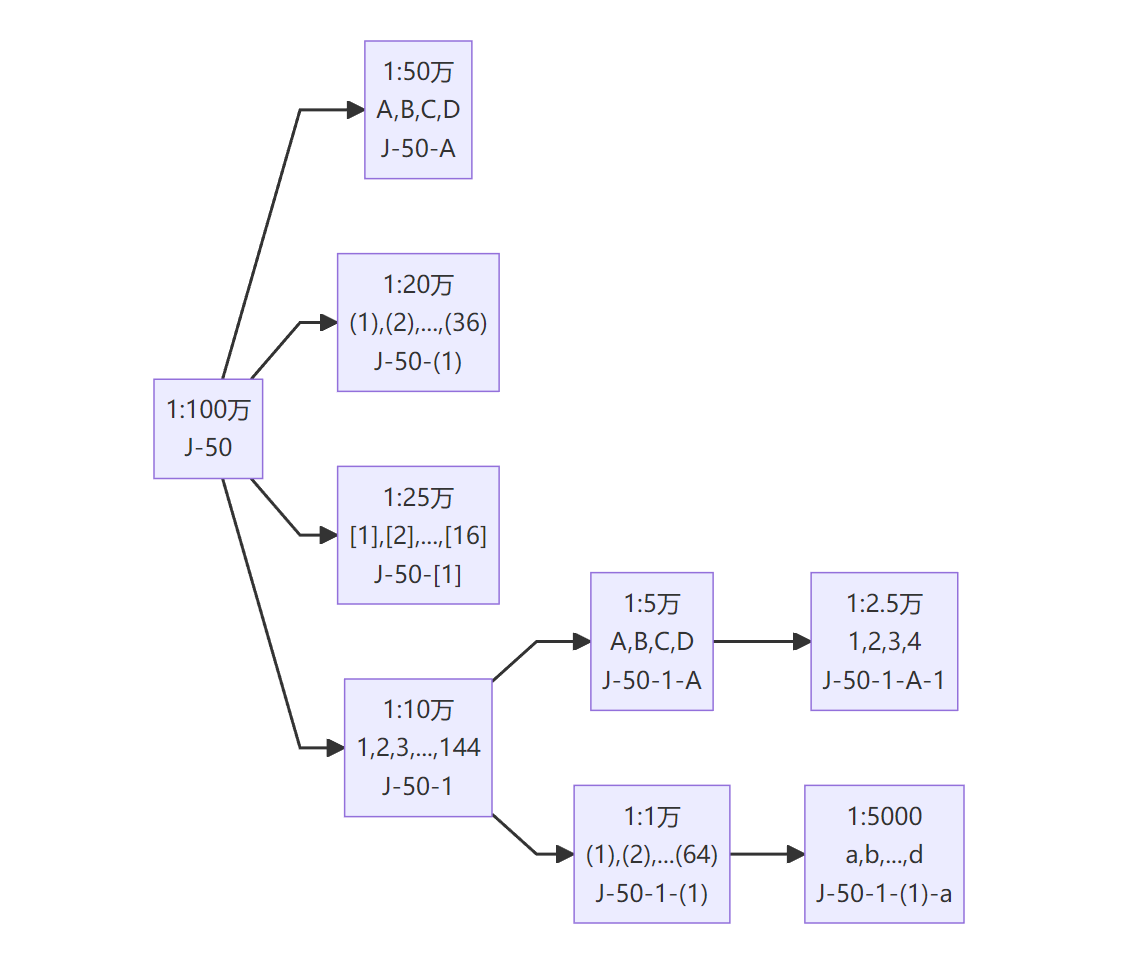
地图投影的基本情况
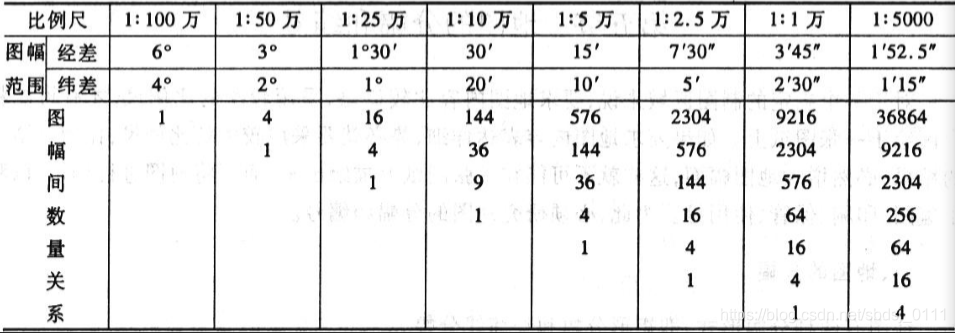
地图投影主要关注从球形表面到平面图的转换过程。比如,在绘制世界地图时,地图投影技术是必不可少的。在国家地理信息部门制作大型全国或全球地图集时,他们必须进行精确的地图投影操作。由于地球是圆形的,而地图是平面的,这种本质上的不同导致了地图投影过程中出现了多种变形。
地图投影旨在奠定地图的数学基础。这就像建造高楼大厦需要坚实的地基。地图投影为地图提供了平面坐标系转换等核心要素。在古代,航海家在绘制航海图时采用的简单投影方法,正是对地图投影早期需求的直观反映。

投影变形
地图投影中,形状变化是难以避免的现象。具体来说,长度上会有比例失真和形状扭曲。以地球仪上的大圆弧为例,当它被投影到平面上,原本稳定的长度就会发生变化。在城市路线图的绘制中,若忽视这种长度扭曲,实际距离可能会被错误地展示。

面积变形问题同样重要。在将各国面积在地图上展现时,由于投影方式的影响,某些国家的面积可能会在视觉上产生误差。例如,格陵兰岛在特定投影下,其面积看起来远超实际,这种现象就是由面积变形引起的。
变形对象的研究
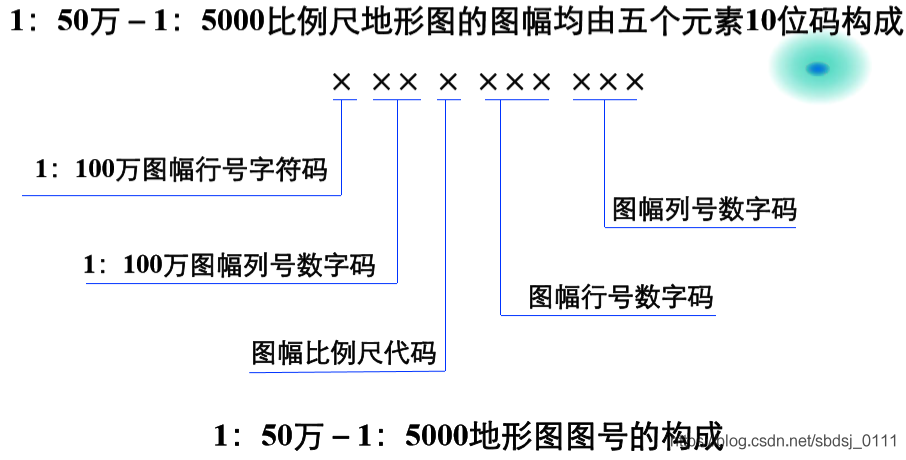
地图投影中的角度扭曲同样属于变形范畴。在制作航空导航图时,若忽略了这种扭曲,飞机的飞行路径角度可能会出错,进而威胁到飞行安全。在精确绘制地图时,投影面上的方向线与原始面的夹角差异是必须加以注意的。
了解标准点和标准线的概念至关重要。在制作某些地区专用地图时,明确这些点与线有助于在一定程度上减轻投影变形所造成的影响。以某城市局部地图为例,若以市中心作为基准点进行投影设计,就能有效降低对城市内部布局的扭曲。
变形椭圆的意义
变形椭圆作为一种分析地图投影变形的实用手段,在制作旅游景区的详细地图时尤为有用。借助它,我们可以清晰地掌握地图投影后的变形状况,从而更好地安排地图的布局。这种椭圆的形状源自将地面上的微分圆按照一定规则投影成椭圆,它直观地呈现了投影过程中产生的变形效果。

研究变形椭圆有助于我们深入了解投影变形的规律。在制作野外地质勘探地图时,通过观察变形椭圆的角度、长度和面积的变化,我们可以对投影方法进行调整,确保地图能够准确展示地质构造的实际情况。
数学关系的核心
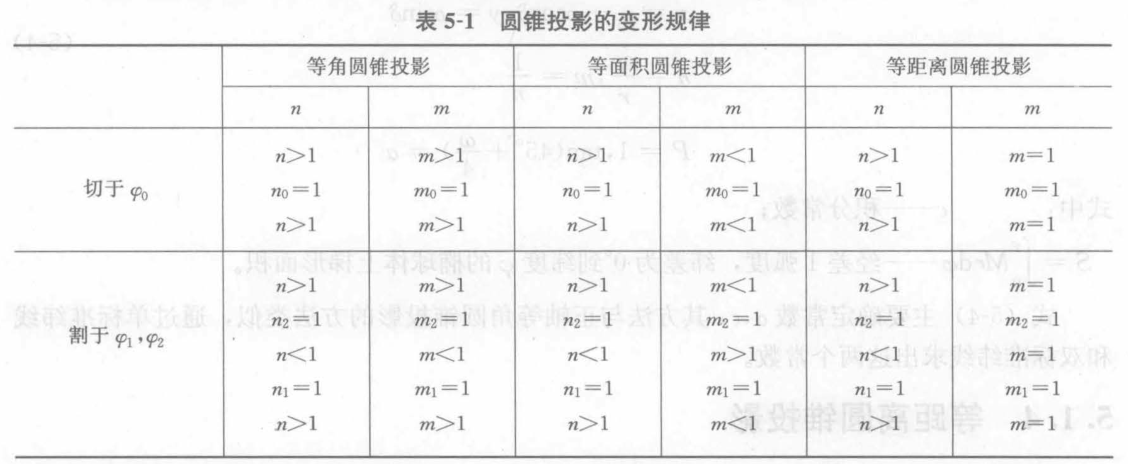
地图投影中,长度比这一数学关系扮演着至关重要的基础角色。在学术研究和高等教育领域,这些数学关系是不可或缺的知识点。它们精确地描述了投影前后线段之间的联系。例如,对于长铁路网线这样的线段,我们可以通过长度比的计算,精确地进行投影,从而在真实长度关系下展现铁路网线的分布。
地图上地理单元面积的正确显示,依赖于面积比计算的准确性。比如,在农业规划地图上,若耕地、林区等面积标注不准确,会极大地影响农业布局及规划的合理性。
地图投影的实际应用
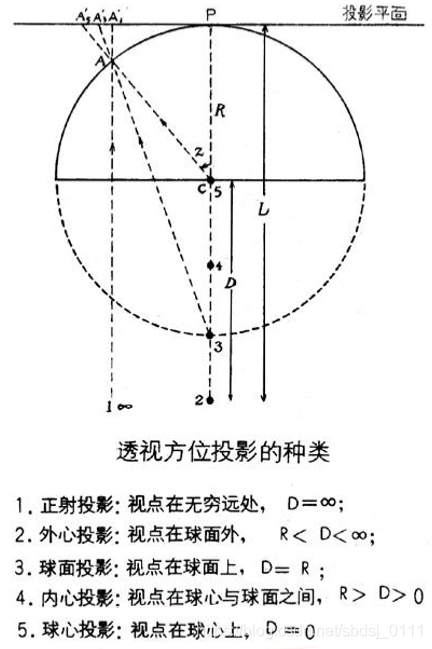
地图在多个领域扮演着不同角色。在军事领域,地形图需要高精度投影来确保作战计划的准确实施。至于气象分析,小区域地图同样需要恰当的投影,以确保气象数据的精确标注和区域关系的正确匹配。
网络地图服务中,用户关注的地图尺度从全球到局部不等。这就要求地图投影技术必须具备灵活性,以适应各种需求。若不然,用户在查询城市中心街道地图时,可能会得到一张严重变形、信息有误的地图。
