文章内容
标准差方法
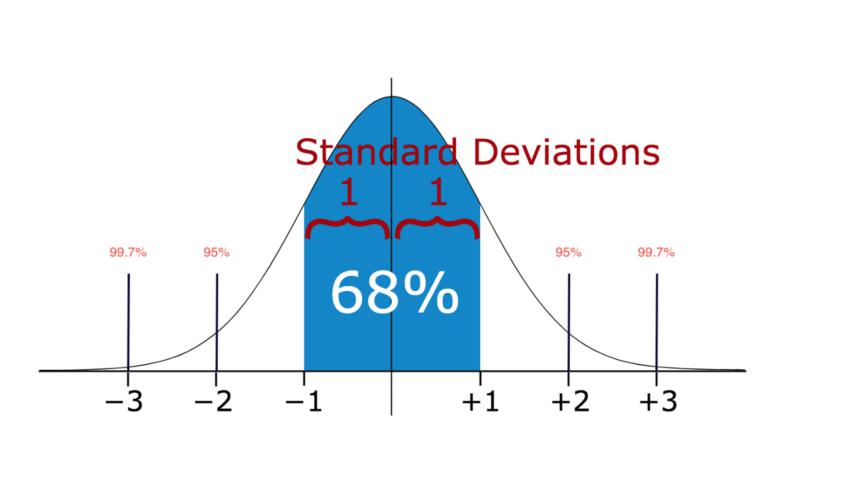
在统计学领域,当数据分布呈正态形态时,其波动会按照特定规律进行。研究发现,约68%的数据集中在了平均值加减一个标准差的范围内,而95%的数据集中在加减两个标准差的范围内,至于99.7%的数据,则分布在加减三个标准差的区间内。
若数据点超出三个标准差的范畴,通常被认为是异常值。这种方法操作简便,对于少量一维数据的初步筛选非常有效,能快速识别出那些明显偏离的数据点。
箱线图方法
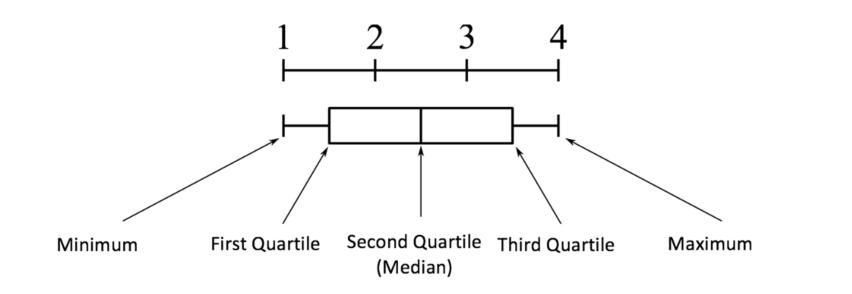
箱线图可以图形化地展示数值型数据,利用分位数来展现数据特征。此法既简单又高效,是直观识别异常值的好方法。
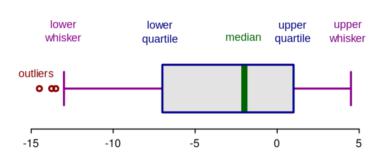
数据点若低于最低界限或超出最高界限,便算作异常情况。这种方法可以直观地展示数据的分布状况。即便是面对大量数据,也能快速锁定异常的数据点。
四分位差方法
确定异常值时,四分位差极为关键。这个差值,确切地讲,就是第三个四分位数与第一个四分位数之间的距离。通过这个距离,我们能够清晰地辨认出哪些数据点属于异常。
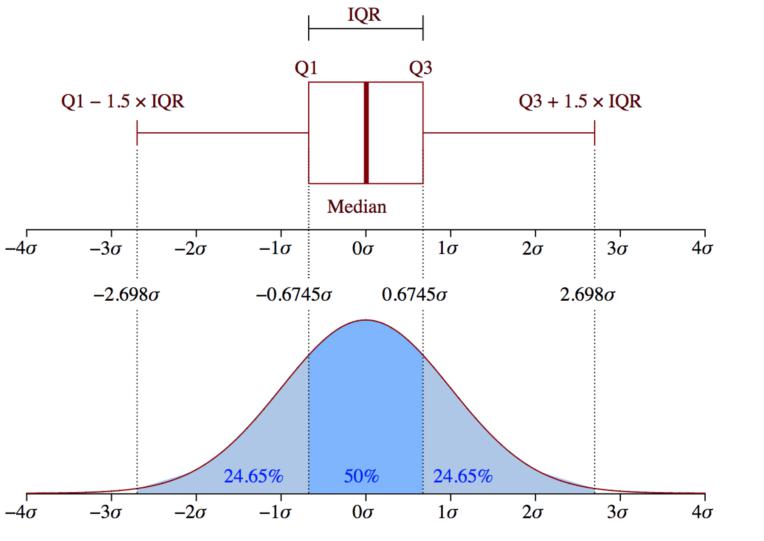
如果数值低于Q1减去四分位距的1.5倍,或者低于箱线图底部的参考点,或者高于Q3加上四分位距的1.5倍,或者高于箱线图顶部的参考点,那么这些观测数据就被认定为异常。此方法结合了数据分位数的有关信息,从而使得对异常值的识别更加全面。
基于密度的异常检测方法
若数据符合高斯分布,我们可以依据标准差来检测异常值。这种方法既适用于一维数据,也适用于多维数据,并且可以根据数据的特性来设定恰当的检测区间。
每个数据都有其适宜的范围,这些范围是可以累加的。若测试数据多数位于这些范围之内,一般被认为是正常的;但若数据量较少且仍在此范围内,可能就表明了异常情况,这在分析复杂数据时特别有帮助。
孤立森林算法
过去的方法一般是在寻找常规区域,会把区域外的数值看作异常。但孤立森林算法的做法不同,它通过找出孤立且不寻常的数据点,不单独给每个数据点打分,以此来形成常规区域。

这一现象说明,异常数值不多,且种类多样,因此在处理高维数据集时有着出色的表现。通过实际应用,这种方法在发现异常数值上非常有效,因此已成为高维数据异常检测领域的一个重要手段。
Robust Random Cut Forest算法
亚马逊运用了一种无需人工监督的算法来检测异常数据,该算法根据数据点的异常分数来执行任务。一般而言,分数较低的数据通常代表正常情况,而分数较高的数据则可能意味着存在异常。
定义“低”和“高”的标准会根据使用环境的不同而有所区别。一般来说,如果一个数值超过了平均值三个标准差,那它就可以被认定为异常。这种算法特别擅长处理高维数据,并且在性能上比孤立森林更出色,它还有自己的一套独特标准。