在数学课堂上,杨辉三角这个图形常常激起学生们浓厚的好奇。它里面藏着许多有趣的规律,而且在我们日常的生活和考试中都能派上用场。现在,我们就来仔细研究一下这个杨辉三角。
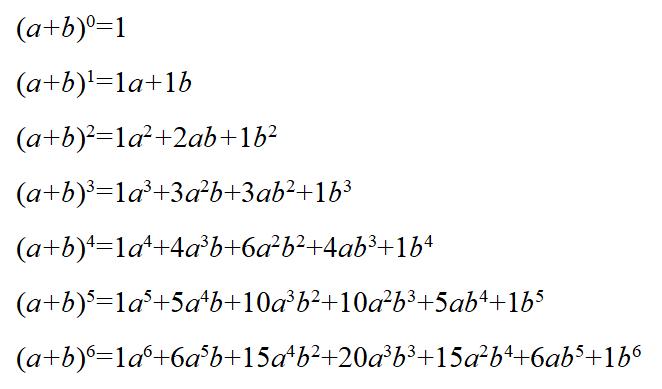

公式表述与类比探究
老师教学生用符号来表示平方公式,并建议他们用类比的方法,观察(a+b≠0)的展开式系数和杨辉三角的数值,以此来探索规律,进而得出展开式系数。这种方法能让学生把已学的知识跟未知的内容联系起来,激发他们的思考,在类比的过程中发现新的知识。
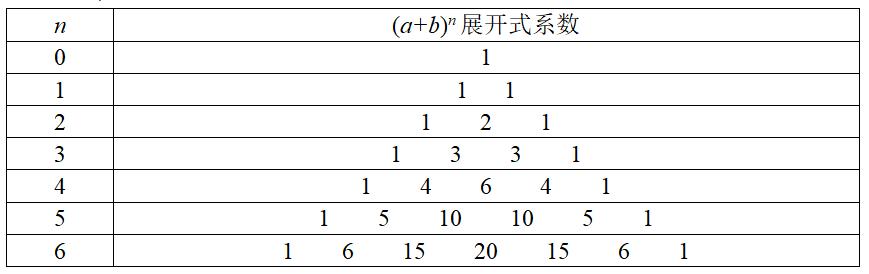
杨辉三角基础规律
学生们在杨辉三角中找到了最关键、最基础的规律,并得到了老师的赞同。他们从“数”与“形”两方面对杨辉三角中的数字关系进行了剖析,这种剖析为将来深入研究其奥秘奠定了牢固的基础,也让人们对这个数学工具的基本构造有了清晰的认识。
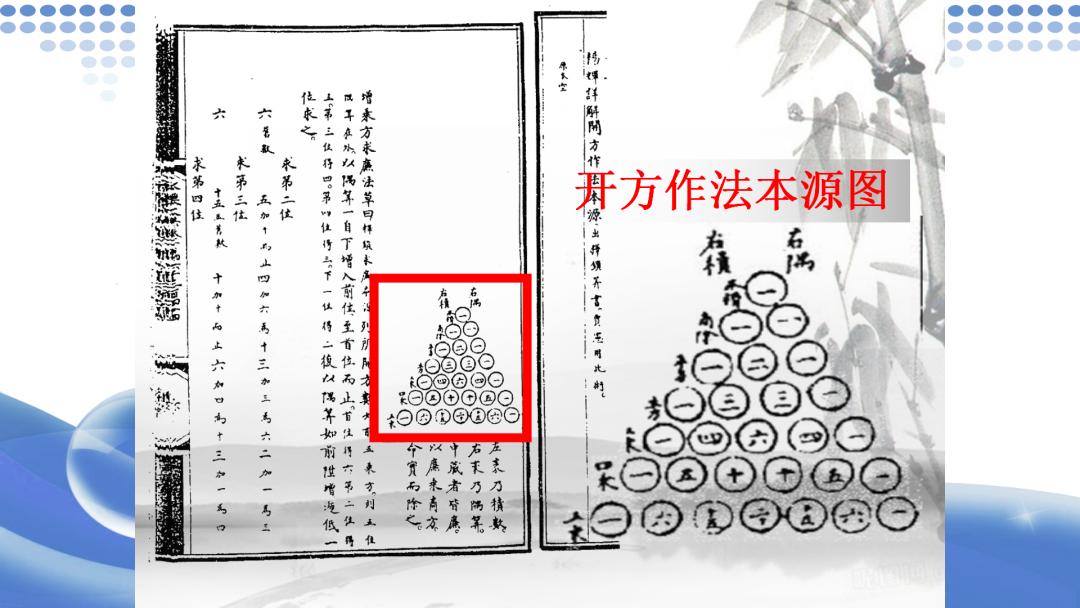
整体看待与斜向特征
老师出了一道关于杨辉三角的题目,引导学生们从全局去理解其中的数字。这一过程拓宽了学生的思维。随后,老师进一步指导他们从斜向视角审视杨辉三角,探寻其斜向特征。这种指导让学生们的视野变得更加宽广,他们学会了从不同角度审视问题,并发现了杨辉三角中那些独特的规律。
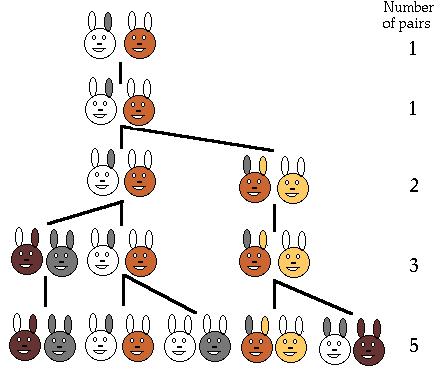
斐波那契数列引出
斐波那契数列在数学领域里很有意思,老师向我们介绍了它的来历,也让我们明白了斐波那契兔子数列的神奇。这让学生们感受到了数学的奇妙,同时也让他们意识到数学与日常生活的紧密关系,以及数学既是生活之源,也是生活之助的道理。

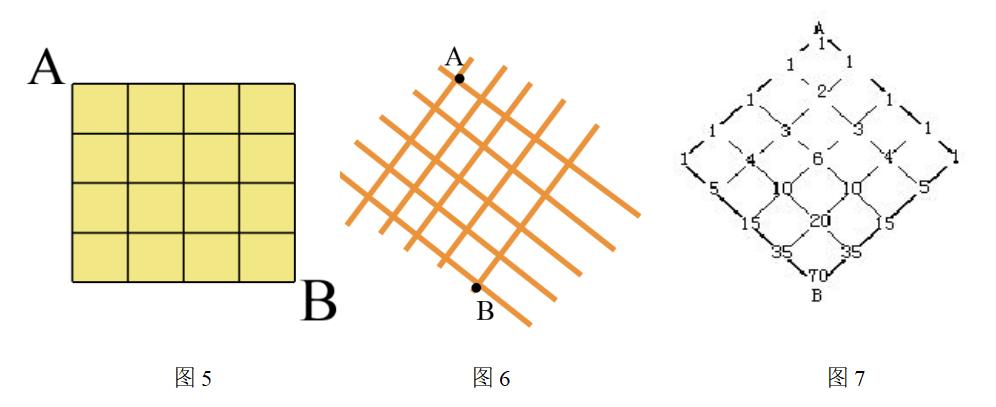
生活实际问题应用
杨辉三角在我们的日常生活中用途广泛。比如,在处理“纵横路线图”这类问题时,它就是一个很好的例子。老师们经常通过这个有趣的问题启发学生思考,并亲自实践去验证,最终得出答案。这种教学方法不仅体现了杨辉三角在解决实际问题中的关键作用,而且也教导了学生们如何将数学知识运用到实际生活中。
考试中的杨辉三角
杨辉三角不仅美观,考试中也会出现相关题型。老师会利用这些题型,帮助学生熟悉考试题型,掌握类比和转换方法。通过学习杨辉三角的规律,学生也能应对考试中的各种难题。
读完这段,你肯定也迫切地想揭开杨辉三角里的神秘规律?何不把你的想法写在评论区?还有,别忘了点赞和分享这篇文章,让更多人感受到数学的魅力!