手机地图上呈现的定位,你可曾知晓,它或许跟实际的GPS坐标存在几百米的差距呢?我国特殊的坐标加密系统隐匿于这背后 。
坐标系的由来
运用的是WGS – 84坐标系乃是 GPS 的情况,此为全球统一的定位标准。在2002年的时候,国家测绘地理信息局推出了GCJ – 02坐标系,针对真实坐标开展了加密处理工作。这样的加密致使国内地图服务商务必要采用处理之后的坐标 。
该体系被高德地图、腾讯地图一类主流应用纷纷采用,其设计初衷是出于国家安全考量,旨在保障敏感地点不会于公开地图上精准呈现,然而,这却给普通用户造成了定位出现偏差的困扰。
火星坐标的特点
GCJ – 02被称作“火星坐标系”,这是由于它能致使坐标点“漂移”至另外一个位置,这种偏移并非固定不变的,于不同地区,其偏移量以及方向都存在差异,虽说偏移范围一般处于几百米以内,然而却足以对定位精度造成影响。
你若运用手机GPS去记录轨迹,便会发觉轨迹点同实际道路存有显著偏差,此偏差于城乡结合部以及新开发区域格外明显,众多运动爱好者于使用运动类APP之时都遭遇过这个问题。
百度坐标的演变

百度公司于GCJ – 02基础之上,更进一步开展了BD – 09坐标系的开发工作,这等同于实施了二次加密行为,致使百度地图同其他国内地图服务商之间的坐标同样存有差异,百度如此行事是为了构建属于自身的坐标体系。
在实际运用当中,百度地图的坐标跟其他地图没办法直接进行互用,举例来说,同个地点的坐标,于百度地图以及高德地图上呈现不一样,这样的差异致使开发者要去做额外的坐标转换工作。
# -*- coding: utf-8 -*-
import json
import math
x_pi = 3.14159265358979324 * 3000.0 / 180.0
pi = 3.1415926535897932384626 # π
a = 6378245.0 # 长半轴
ee = 0.00669342162296594323 # 扁率
def wgs84togcj02(lng, lat):
"""
WGS84转GCJ02(火星坐标系)
:param lng:WGS84坐标系的经度
:param lat:WGS84坐标系的纬度
:return:
"""
if out_of_china(lng, lat): # 判断是否在国内
return lng, lat
dlat = transformlat(lng - 105.0, lat - 35.0)
dlng = transformlng(lng - 105.0, lat - 35.0)
radlat = lat / 180.0 * pi
magic = math.sin(radlat)
magic = 1 - ee * magic * magic
sqrtmagic = math.sqrt(magic)
dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * pi)
dlng = (dlng * 180.0) / (a / sqrtmagic * math.cos(radlat) * pi)
mglat = lat + dlat
mglng = lng + dlng
return [mglng, mglat]
def gcj02towgs84(lng, lat):
"""
GCJ02(火星坐标系)转GPS84
:param lng:火星坐标系的经度
:param lat:火星坐标系纬度
:return:
"""
if out_of_china(lng, lat):
return lng, lat
dlat = transformlat(lng - 105.0, lat - 35.0)
dlng = transformlng(lng - 105.0, lat - 35.0)
radlat = lat / 180.0 * pi
magic = math.sin(radlat)
magic = 1 - ee * magic * magic
sqrtmagic = math.sqrt(magic)
dlat = (dlat * 180.0) / ((a * (1 - ee)) / (magic * sqrtmagic) * pi)
dlng = (dlng * 180.0) / (a / sqrtmagic * math.cos(radlat) * pi)
mglat = lat + dlat
mglng = lng + dlng
return [lng * 2 - mglng, lat * 2 - mglat]
def transformlat(lng, lat):
ret = -100.0 + 2.0 * lng + 3.0 * lat + 0.2 * lat * lat +
0.1 * lng * lat + 0.2 * math.sqrt(math.fabs(lng))
ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *
math.sin(2.0 * lng * pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(lat * pi) + 40.0 *
math.sin(lat / 3.0 * pi)) * 2.0 / 3.0
ret += (160.0 * math.sin(lat / 12.0 * pi) + 320 *
math.sin(lat * pi / 30.0)) * 2.0 / 3.0
return ret
def transformlng(lng, lat):
ret = 300.0 + lng + 2.0 * lat + 0.1 * lng * lng +
0.1 * lng * lat + 0.1 * math.sqrt(math.fabs(lng))
ret += (20.0 * math.sin(6.0 * lng * pi) + 20.0 *
math.sin(2.0 * lng * pi)) * 2.0 / 3.0
ret += (20.0 * math.sin(lng * pi) + 40.0 *
math.sin(lng / 3.0 * pi)) * 2.0 / 3.0
ret += (150.0 * math.sin(lng / 12.0 * pi) + 300.0 *
math.sin(lng / 30.0 * pi)) * 2.0 / 3.0
return ret
def out_of_china(lng, lat):
"""
判断是否在国内,不在国内不做偏移
:param lng:
:param lat:
:return:
"""
if lng 137.8347:
return True
if lat 55.8271:
return True
return False
if __name__ == '__main__':
[lng,lat]=[114.061202,22.529388]
[dstlng, dstlat] = gcj02towgs84(lng, lat)
print(dstlng, dstlat)转换原理分析
去到WGS – 84自GCJ – 02进行回转,这是需特定转换算法的事情,此算法并非简单的那种关乎加减的基本运算,而是有着复杂的非线性变换融合其中,转换公式那边要考虑经纬度之间的相互影响状况,并且不同区域其参数也是存在不同之处的。
算法的核心之处在于把加密过程进行逆向的运算从而去还原真实的坐标,然而因为加密的时候将随机扰动给加入了进去,所以完全精确地实现还原并非是容易做到的的事情,当下公开出来的转换方法能够达成米级的精度,总体上满足日常的需求。
实际应用案例
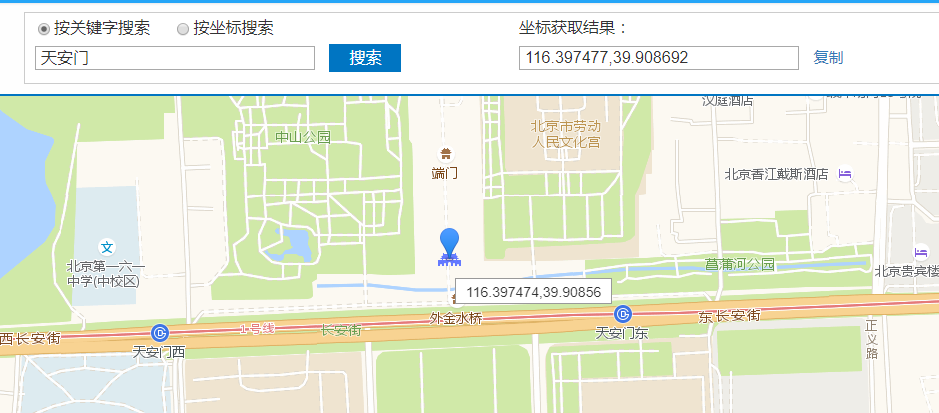
以北京天安门作为例子,它的GCJ – 02坐标是116.397477 ,39.908692 。转换成为WGS – 84坐标以后变成116.391233 ,39.907288 。两地的坐标相差大概600米,这样的距离在实际的导航当中会产生明显的影响。
要是你于Google Earth上查看天安门所处位置,那是得运用转换之后的WGS – 84坐标的。直接去输入高德地图所显示的坐标,这会致使位置出现错误。此例子相当好地表明了坐标转换的必要性。
开发者注意事项
开发跟地图有关的应用之际,一定要留意坐标系的统一呀,去采集GPS数据之时,得明确所使用的坐标系呢,当在不同平台之间传输坐标数据之时,要开展转换操作哟,要是忽略了这个问题,将会致使位置信息出现极为严重的错误啦。
提议于代码之内融入已然成熟的坐标转换库,像是proj4或者gcoord之类的。这些库历经了长达许久的测试,能够应对各种各样的边缘状况。与此同时要妥善做好数据源的记录,标明每一个坐标所运用的坐标系。
要是你在运用地图应用之际,有没有碰到过因坐标存在偏差而致使的导航出现差错的情况呢?欢欢喜喜在评论区去分享你所经历的事儿,要是感觉这篇文章有着一定帮助的话,那就请点个赞予以支持吧!