在精准预测的探求之路上,损失函数犹如指向迷途指明灯,引导模型驶离数据浩渺之洋,向最精巧的预测小岛进发。今日,让我们携手深入这一精妙且引人入胜的领域,详细解析分类与回归任务中所运用的各类损失函数——包括均方差损失至交叉熵损失在内,它们各自散发出独特风采并发挥着重要作用。
均方差损失:预测的精确度量
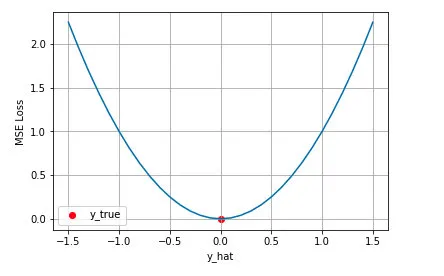
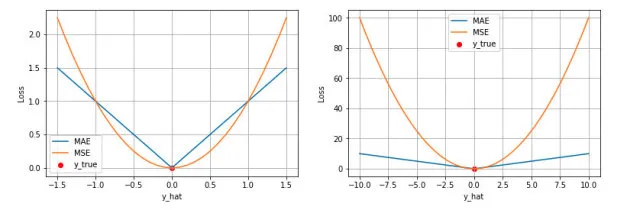
在回归问题中,均方差损失(MSE)被广泛采用,这主要得益于其简洁且强大的特性——作为度量模型预测值与真实值偏差的精准标尺,其计算方式是将全部预测误差平方后求总和,然后取平均值。这种方法的显著优点在于,它能加大对较大误差的惩罚力度,从而引导模型朝更精确的方向进行优化。试想,当我们构建一个用于预测气温的模型时,MSE就如同那个时刻提醒我们“更精确些,更精确些”的声音。
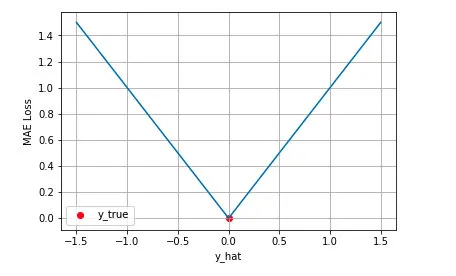
平均绝对误差损失:误差的直截了当
相较于MSE,均方根误差损失(RootMeanSquaredError,RMSE)以更直观的方法度量误差。RMSE实质上计算了预测值与实际值间差异的平方和的算术平均数,能有效地抵抗数据集内异常值的干扰,因此在数据分布复杂且含有大量异常点的情况下,RMSE可能成为更优的选择。RMSE如同坦诚的朋友,直接揭示误差的大小。
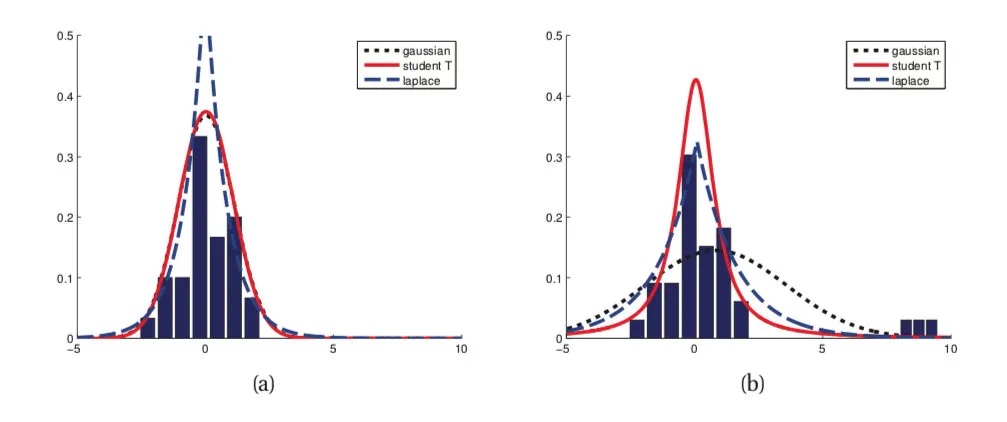
HuberLoss:结合两者的优点
HuberLoss巧妙地融合了MSE与MAE的优越性。小型误差环境下,它显现出类似于MSE的特性,确保损失函数的光滑可导;然而,当误差增大时,HuberLoss会切换至MAE模式,以降低异常值的干扰。HuberLoss犹如一位精明的决策者,既擅长精准计算,也能从容应对各种突发状况,无论环境如何变幻莫测,始终保持冷静且高效。
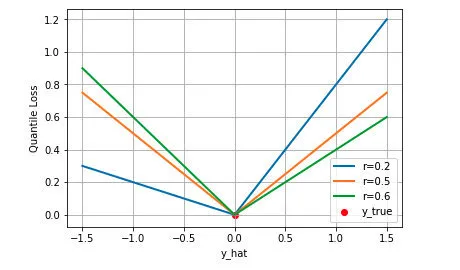
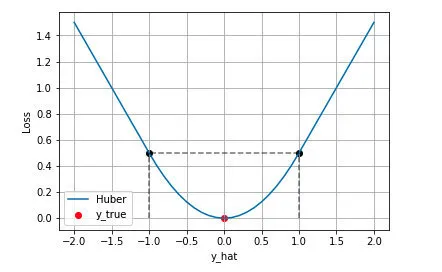
分位数损失:不仅仅是中位数
分位数回归作为一种精密的回归策略,不仅能预估目标值的期望或中位数,更可根据需求设定不同的分位数进行拟合。而分位数损失则是实现此功能的关键手段。通过调整分位数系数,我们得以获取不同置信度的预测区间,这对于风险控制与金融预测具有重大意义。分位数损失犹如一个多维视角的观察者,协助我们全方位地解读数据。
交叉熵损失:分类问题的灵魂
论及如何为分类问题选择损失函数时,交叉熵损失无疑为最佳之选。无论面临二分类还是多分类挑战,该损失函数均可准确度量出模型预测概率分布与实际分布间的差距。优异的表现源自于其深厚的信息理论基础,实质上,它在计算准确传达真实标签所需的最少比特数。因此,交叉熵损失犹如一位精明的分析师,能精准评估信息价值,助我们在错综复杂的数据环境中找寻正确的道路。
Hinge损失:支持向量机的利剑
首先,不可忽视的是支持向量机(SVM)中的核心元素——“HingeLoss”。该损失函数旨在激励模型建立可靠的预测边界,使正负实例间拥有充足的差异。尤其适用于线性不可分问题,犹如严格坚持原则且不容含糊的守门者。
本文对机器学习中多种关键性的损失函数进行了深度剖析,它们各有特定作用与重要性,成为构建优秀AI模型所需之基础。从基本的线性回归至高级的分类算法,映射出损失函数在模型优化中的重要地位。那么作为一位数据科学家,你将如何运用并调整这些损失函数以提升模型的性能呢?热切期待您分享宝贵经验及观点!