压缩算法：节省空间和时间的神奇魔法

本文深入探讨了怎样透过高效压缩技术对二进位比特序列进行优化，提高信息的存储及传输效率。借助BinaryStdIn及BinaryStdOut两套工具，我们得以实现比特数据的精确读写与计算机识别码的转换。

public static void compress(){
    Alphabet DNA=new Alphabet("ACTG");
    String s=BinaryStdIn.readString();
    int N=s.length();
    BinaryStdOut.write(N);
    
    for(int i=0;i<N;i++){
        int d=DNA.toIndex(s.charAt(i));
        BinaryStdOut.write(d,DNA.lgR());
    }
    BinaryStdOut.close();
}

比特流的读取与写入

public static void expand(){
    Alphabet DNA=new Alphabet("ACTG");
    int w=DNA.lgR();
    int N=BinaryStdIn.readInt();
    for(int i=0;i<N;i++){
        char c=BinaryStdIn.readChar(w);
        StdOut.println("c="+c);
        char e=DNA.toChar(c);
        StdOut.println("e="+e);
        BinaryStdOut.write(DNA.toChar(c));
    }
    BinaryStdOut.close();
}

在计算机科学领域中，二进制位被视为信息的最小单元。通过采用BinarystdIn.readBoolean()方法解析布尔值，看似简单的流程蕴含着深厚的信息处理智慧。此项技术能够精准地从二进制数据流中获取所需信息，并予以清晰化呈现。另一方面，借助于BinaryStdOut.write(booleanb)方法，我们可以将获取到的信息重新编码为二进制流，从而实现数据的有效输出。正是凭借这些输入输出操作，计算机得以灵活应对各类数据处理与存储任务。每读取两位二进制位并将其转化为整数值的策略，不仅提高了效率，更极大地加速了数据处理进程。

00000000000000000000000000000000
00000000000000000000000000000000
00000000000000011111110000000000
00000000000011111111111111100000
00000000001111000011111111100000
00000000111100000000011111100000
00000001110000000000001111100000
00000011110000000000001111100000
00000111100000000000001111100000
00001111000000000000001111100000
00001111000000000000001111100000
00011110000000000000001111100000
00011110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111110000000000000001111100000
00111111000000000000001111100000
00111111000000000000001111100000
00011111100000000000001111100000
00011111100000000000001111100000
00001111110000000000001111100000
00001111111000000000001111100000
00000111111100000000001111100000
00000011111111000000011111100000
00000001111111111111111111100000
00000000011111111111001111100000
00000000000011111000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000001111100000
00000000000000000000011111110000
00000000000000000011111111111100
00000000000000000111111111111110
00000000000000000000000000000000
00000000000000000000000000000000

比特传输中，不可避免地存在大量重叠的数据，这正是游程编码得以运用的重要契机，它可以凭此对信息进行高效的压缩处理。游程编码主要借助数据冗余特征，通过巧妙地将重复的0/1序列转化为相应的数值，以达到节省存储空间的目的。例如，连续的0和1可以被简化为10,4,4,9,5，这样的精炼方式极大地降低了数据冗余。在实践中，游程编码尤其适用于位图压缩，对于提高存储与传输效率有着显著的作用。

00000000001111000011111111100000

游程编码的魅力

public static void compress() {
    char cnt = 0;
    boolean b, old = false;
    while (!BinaryStdIn.isEmpty()) {
        b = BinaryStdIn.readBoolean();
        if (b != old) {
            BinaryStdOut.write(cnt);
            cnt = 0;
            old = !old;
        } else {
            if (cnt == 255) {
                BinaryStdOut.write(cnt);
                cnt = 0;
                BinaryStdOut.write(cnt);
            }
        }
        cnt++;
    }
    BinaryStdOut.write(cnt);
    BinaryStdOut.close();
}

游程编码在去除数据冗余及处理大容量数据（尤其是图像）上表现突出，它能够将像素集合中相同的部分简化成特定的数字表示，从而大大节约存储空间。然而，值得注意的是，此种编码并非万能之策，对于包含大量符号和词汇的自然语言文件（如英文文档），其效果可能不甚明显。这主要源于此类文本中字符出现频率差异较大，导致长游程现象较少。

public static void expand() {
    boolean b = false;
    while (!BinaryStdIn.isEmpty()) {
        char cnt = BinaryStdIn.readChar();
        for (int i = 0; i < cnt; i++)
            BinaryStdOut.write(b);
        b = !b;
    }
    BinaryStdOut.close();
}

霍夫曼（Huffman）压缩与LZW压缩均基于相同原则——在保持同等空间利用的基础上，精简高频字符的占用空间，并借助冗余内容补充低频字符之不足。霍夫曼算法通过改进最佳单词查找树结构，进一步提升压缩效率。每当新数据流入，该算法将根据字符出现频率对查找树进行实时更新，从而实现更高效的压缩效果。这种智能化设计不仅提高了压缩效率，还使数据存储更加科学合理。

霍夫曼压缩的独特之处

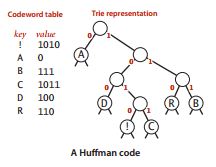
A:0
B:1
R:00
C:01
D:10

霍夫曼压缩法因卓越的编码效率与极高的压缩率而受到业界的普遍好评。其核心在于建立字符频率表，以实现对每个字符最佳的比特分配策略。编码过程中，通过优先遍历查找树，将内层节点设为0，叶节点设为1，并附加上相应的ASCII码。正是这种独特的编码技术，使文件压缩效果显著，且解压后能够快速恢复。

压缩过程中，利用先进的比特流分析技巧，对词汇查找树进行重构，解析并提取节点特征，以此保证霍夫曼压缩过程高效稳定。此策略充分满足了数据传输存储的需求。霍夫曼压缩的独特之处在于将固定长度数据转换为可变长度编码，极大提升了数据压缩领域的性能水平。

LZW压缩的定长编译表

public static class Node implements Comparable {
    private char ch;
    private int freq;
    private final Node left, right;
    Node(char ch, int freq, Node left, Node right) {
        this.ch = ch;
        this.freq = freq;
        this.left = left;
        this.right = right;
    }
    public boolean isLeaf() {
        return left == null && right == null;
    }
    public int compareTo(Node that) {
        return this.freq - that.freq;
    }
}

相较于霍夫曼压缩方法，LZW压缩算法以固定长度码表为编码根基，成功化解了变长编码的困扰。通过精心构建字符与编码位数值之间的符号表，大幅提升了解压效率以及数据压缩比率。优越的符号表功能使得只需依靠编码位数值，便能快速定位到相应字符，从而实现高效率的数据恢复。LZW的核心策略在于利用已有的字符模式来生成新的编码，特别适合于文本及其他自然语言文件的压缩处理。

private static Node buildTrie(int[] freq) {
    MinPQ pq = new MinPQ();
    for (char c = 0; c  0)
            pq.insert(new Node(c, freq[c], null, null));
    while (pq.size() > 1) {
        Node x = pq.delMin();
        Node y = pq.delMin();
        Node parent = new Node('', x.freq + y.freq, x, y);
        pq.insert(parent);
    }
    return pq.delMin();
}

迈入新时代，当代计算机运用高效算法处理比特流，如行程编码、霍夫曼压缩及LZW压缩等，大幅度提升存储效果和压缩比。故而，深入掌握数据压缩之秘诀至关重要。对于比特流的奥妙之处，您是否心生向往？欢迎在评论区发表见解，同时请为本文点赞并分享，让更多人有幸探索此神秘领域的魅力！

private static void writeTrie(Node x) {
    if (x.isLeaf()) {
        BinaryStdOut.write(true);
        BinaryStdOut.write(x.ch);
        return;
    }
    BinaryStdOut.write(false);
    writeTrie(x.left);
    writeTrie(x.right);
}