在项目执行过程中,常常会遇到坐标不一致的情况,尤其是在坐标类型、椭球形状、投影方式等方面,这些差异出现的频率较高。那么,关于坐标转换的细节又是怎样的?其中又有哪些方法和窍门?让我们共同来深入了解一番。
坐标差异常见现象
在众多项目中,资料里包含的坐标数据十分复杂,包括大地经纬度坐标和平面坐标等。这些多样的坐标种类在后续工作中可能导致误差。此外,所使用的椭球体和投影技术也各不相同。比如,不同地区可能会根据地形特点选择不同的椭球体,而投影方法则会根据实际需求进行挑选。
坐标转换普遍应用
众多项目中,坐标系的转换应用极为普遍。这种转换包括将地面坐标转换成平面坐标,将平面坐标转换成空间直角坐标,还有将平面坐标转换回地面坐标等多种类型。在工程领域,从建筑设计到地图绘制,这些坐标转换都是必不可少的环节。以高铁建设为例,为确保坐标数据的精准,各个施工环节可能需采用不同类型的坐标,故而坐标转换的工作显得尤为关键。
无转换参数奥秘
这里所说的无转换参数并不是真的无需考虑,实际上在确定源坐标系与目标坐标系所依据的参考椭球体参数时,转换关系已经确定无疑,这种隐含的转换关系我们称之为“隐性转换参数”。以津巴为例,该国采用WGS84参考椭球的经纬度坐标系统。若要将这些坐标转换至ARC50坐标系下的平面直角坐标,虽然转换过程中没有直接的显式参数,但WGS84参考椭球本身已经为我们指明了转换的具体规则。
坐标转换理论验证
在理论探讨中,我们通常将经纬度数值转换成平面坐标,随后再将这些坐标转换回经纬度数值,理想情况下这些数值应当保持一致。但实际情况中,由于各种因素,可能会有细微的误差产生。在科学研究的实践中,这一理论常被用作评估坐标转换软件精确度的标准,软件输出的结果越接近理论数值,就越能证明其具有较高的可靠性。
七参作用详解
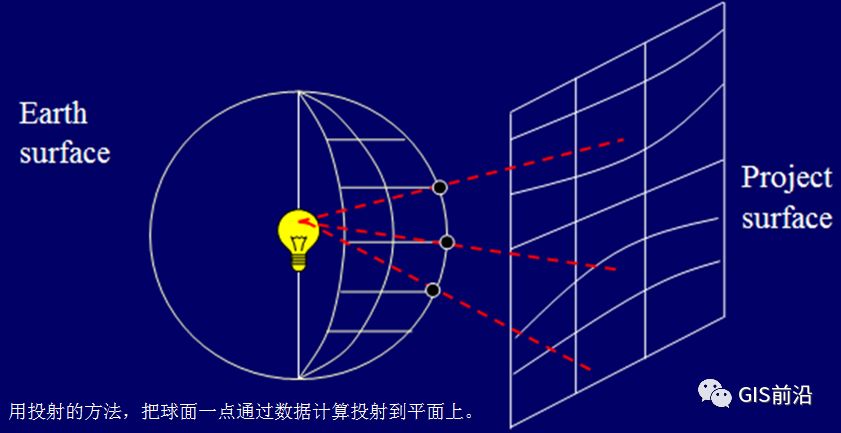
两个坐标系之间的转动、移动和缩放需要七个核心数值。在这七个数值中,移动操作关联着Dx、Dy、DZ三个维度的变动,转动也有三个相关数值,而缩放操作则额外多出一个数值。通过这七个数值,我们可以实现一个坐标系的转换,使其成为目标坐标系。在地理信息系统整合跨国或广泛区域的数据时,这七个数值发挥着极其重要的作用。
三参四参特点
XYZ三个坐标轴若保持同向,转换只需进行平移,此时涉及三个参数;若缩放比例等于1,那么这种三参数转换便成为七参数转换的一种特定情形。至于四参数转换,它适用于椭球体内不同坐标系间的转换,涵盖了X轴和Y轴的平移、旋转角度以及比例因子,而且因为它不涉及高程的调整,所以特别适合用于平面坐标的转换。在城市地理测绘的特定局部,四参数转换技术较为普遍,它能够有效地进行坐标转换操作。
我想咨询大家,在你们参与的项目执行过程中,是否遭遇过特别棘手的坐标转换挑战?如果这篇文章对您有所启发,还请记得点赞并分享给更多人!